Monthly Archives: December 2020

For each virus node, count how many normal it connects. By doing dfs, if a normal connects to another virus node, then branch from this normal node won’t count.

In below case, there are 2 virus node [0, 5]. node 1 can connect with [1, 2, 8, 9]. 5 can connect with [6, 7]. [3, 4] connects to 2 virus node, so they won’t be counted.

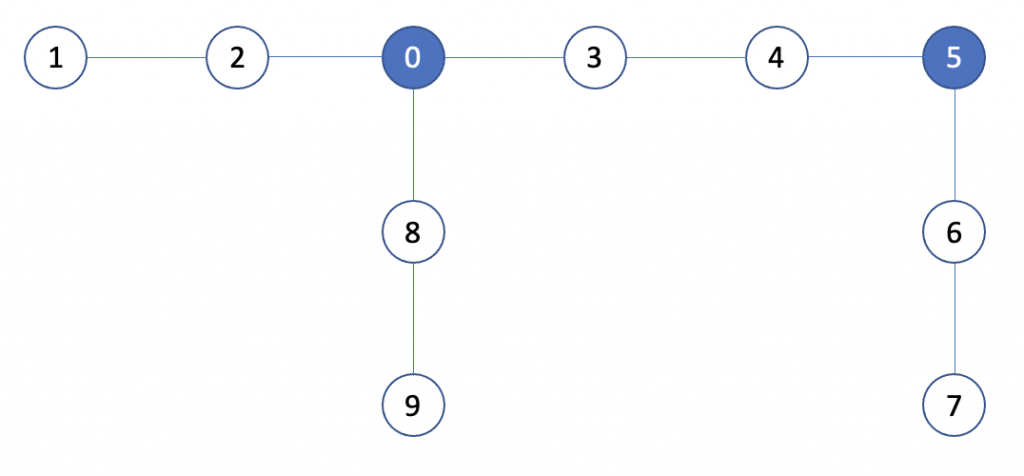
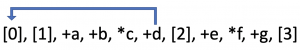Assume there are 4 points in first group, labeled with 0, 1, 2, 3. 3 points in second group, labeled with A, B, C.

Define dp[i][j]. Use binary to symbolize j, for example dp[2][6] = dp[2][(110)]. This means minimum cost for first 3 (0, 1, 2) points in first group connecting with B, C points in second group. In another way, write it like dp[2][CB*]

dp[3][C*A] = min{
dp[3][**A] + cost[3][C],  // make a new connection in same row
dp[3][C**] + cost[3][A],
dp[2][**A] + cost[3][C],     // no C in row 2, C is new in row 3. build connection 3->C
dp[2][C**] + cost[3][A],
dp[2][C*A] + cost[3][C],    // CA is already included in row2, reuse C in row 3.
dp[2][C*A] + cost[3][A]
}

Code:

public static int connectTwoGroups(List<List<Integer>> cost) {
    int col = cost.get(0).size();
    int[][] memo = new int[cost.size()][1 << col];
    for (int[] m : memo) {
        Arrays.fill(m, Integer.MAX_VALUE);
    }
    dfs(cost.size() - 1, (1 << col) - 1, memo, cost);
    return dfs(cost.size() - 1, (1 << col) - 1, memo, cost);
}

private static int dfs(int row, int b, int[][] memo, List<List<Integer>> cost) {
    if (memo[row][b] != Integer.MAX_VALUE) {
        return memo[row][b];
    }
    if ((b - (b & (-b))) == 0) {    // b only has 1 one in binary
        int col = 0;
        while ((b & (1 << col)) == 0) {
            col++;
        }
        memo[row][b] = 0;
        for (int i = 0; i <= row; i++) {
            memo[row][b] += cost.get(i).get(col);
        }
        return memo[row][b];
    }
    if (row == 0) {
        memo[row][b] = 0;
        for (int i = 0; i < cost.get(0).size(); i++) {
            if ((b & (1 << i)) > 0) {
                memo[row][b] += cost.get(0).get(i);
            }
        }
        return memo[row][b];
    }
    for (int col = 0; col < cost.get(0).size(); col++) {
        if ((b & (1 << col)) > 0) {
            memo[row][b] = Math.min(memo[row][b], dfs(row, b - (1 << col), memo, cost) + cost.get(row).get(col));
            memo[row][b] = Math.min(memo[row][b], dfs(row - 1, b - (1 << col), memo, cost) + cost.get(row).get(col));
            memo[row][b] = Math.min(memo[row][b], dfs(row - 1, b, memo, cost) + cost.get(row).get(col));
        }
    }
    return memo[row][b];
}

at [2],
mult=c
add=((a+b)*c+d)

From [0] to [2], adding change operation of +a, +b, *c, +d, it needs apply [0]*mult + add

Reversely, from [2] to [0], to calculate back with +a, +b, *c, +d, it needs apply ([2] – add) / mult

In all, the calculation is like when appending each value, calculate back by removing the operations before. Let it start from very beginning without any operation. Then in the end after all operations,  when getIndex, calculate forwardly with current mult, add

(a / b) % mod = (a * x) % mod

Here, x is inverse modular of b. In Java,

x = BigInteger.valueOf(a).modInverse(BigInteger.valueOf(mod)).longValue();

https://www.bilibili.com/video/av970029359/