Logistic Regression answer the YES/NO question. For example, giving a set of size of tumor, it answers if it is a tumor. Giving height and weight of a person, answer if it is a man.
Hypothesis
We have hypothesis function ![]() , and it ranges
, and it ranges ![]() . And we define the answer is YES when hypothesis is greater than 0.5, else is NO.
. And we define the answer is YES when hypothesis is greater than 0.5, else is NO.
 .
.
First, let’s take a look at the shape of logistic function(sigmoid function) g(z).
![]()
It is like:
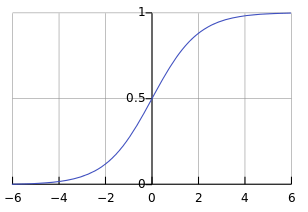
We found that this function can satisfy our need. g(z) ranges from (0, 1).
We have z>=0 –> g(z)>=0.5 –> predict y=1,
And we have z<0 –> g(z)<0.5 –> predict y=0
Having chose the logistic function, let’s define hypothesis for logistic regression:
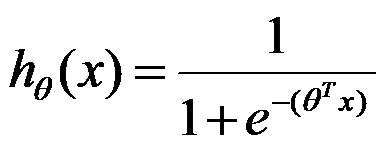
Let’s do some analysis. When ![]() , we have
, we have 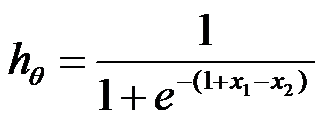 .
.
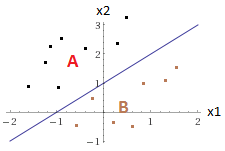
For this hypothesis, we know when 1+x1-x2>=0, hypothesis is equal to or greater than 0.5, prediction is YES; else hypothesis is less than 0.5, prediction is NO. Take a look at below picture, we know when the point is from region A, the answer is YES; when the point is from region B, the answer is NO.
Another example, when ![]() , we have
, we have 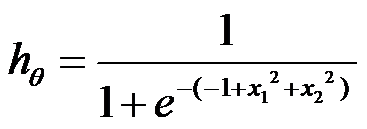 .
.
For this hypothesis, we know when x1^2 + x2^2>=1, hypothesis is equal to or greater than 0.5, prediction is YES; else hypothesis is less than 0.5, prediction is NO. Take a look at below picture, we know when the point is from region A, the answer is YES; when the point is from region B, the answer is NO.

Cost function
Cost function for logistic regression is:
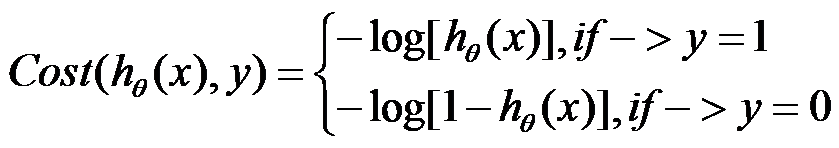
For y=1 case, if the hypothesis is is close to 0, we know the cost function will be close to positive infinity. If hypothesis is close to 1, then cost function will be close to 0.
For y=0 case, if the hypothesis is is close to 0, we know the cost function will be close to 0. If hypothesis is close to 1, then cost function will be close to positive infinity.
Furthermore, cost function can be rewritten as:
![]()
And J of theta can be written as:
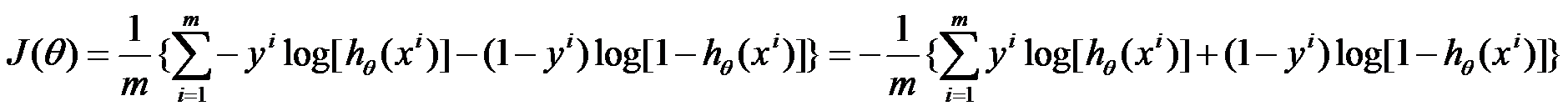
Since we have the cost function, we can solve the logistic regression by gradient descent, repeating below loop until theta becomes to a value which is small enough.
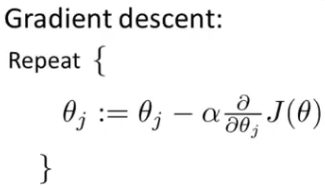
Or logistic regression can be solved by some optimization algorithms(Conjugate gradient, BFGS or L-BFGS).
Learning materials: Andrew NG Machine Learning course.