I’m learning machine learning these days. Here let me write down the note for this.
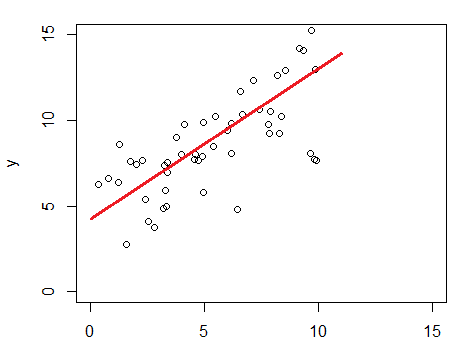
Suppose we have m training points 
in x-y coordination, and we want to find the best line fit for these points .
Since it is the simplest line, we can define the line function, and call it hypothesis:
.
A way to measure how well a line fit these points is least square mean. And we call it loss function:
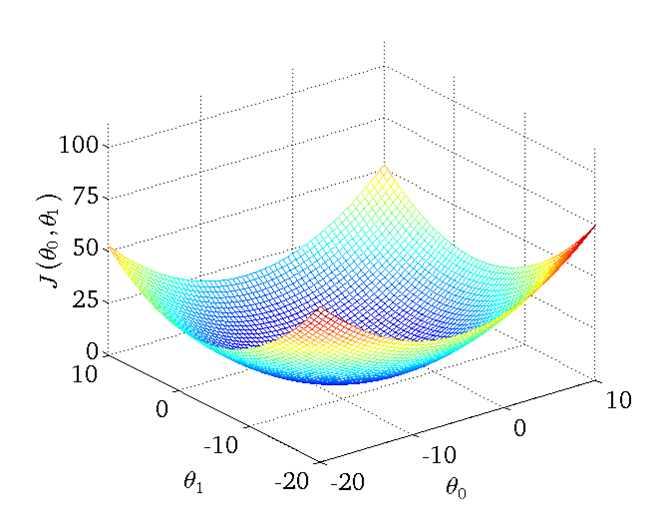
Now, the problem turns to find the 
which the loss function has the minimum value. As said by Andrew NG, the fortunate thing is that the loss function of linear regression are all bowl shape, which mean it always has a extreme value.
One way to minimize the loss function is to use gradient descent algorithm. The basic idea is to let the point on the surface go through gradient direction, in this way, it will finally reach the extreme value. Partial derivative functions for loss function:
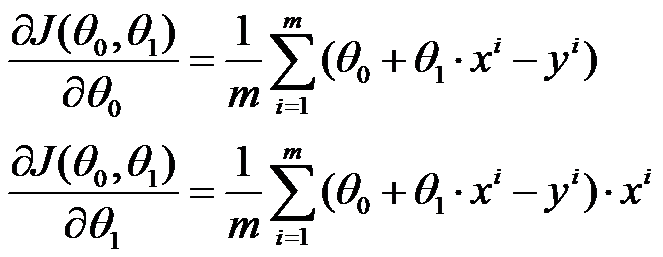
After we got the partial derivative function, we do below until loss function is less than 
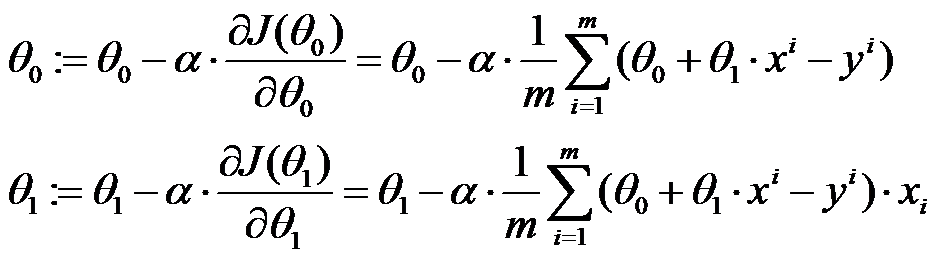
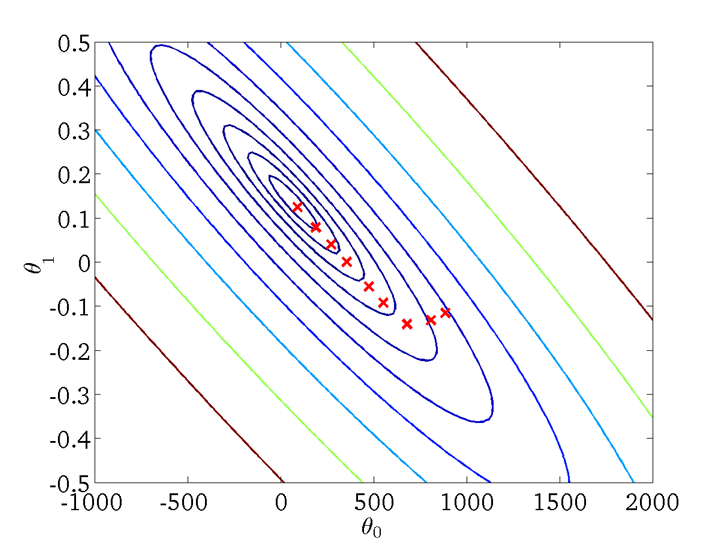
When the loss function is getting close the extreme value, we can see the is moving to the extreme value from the gradient direction.
