Let’s talk about this function:
![]()
It has shape like this:
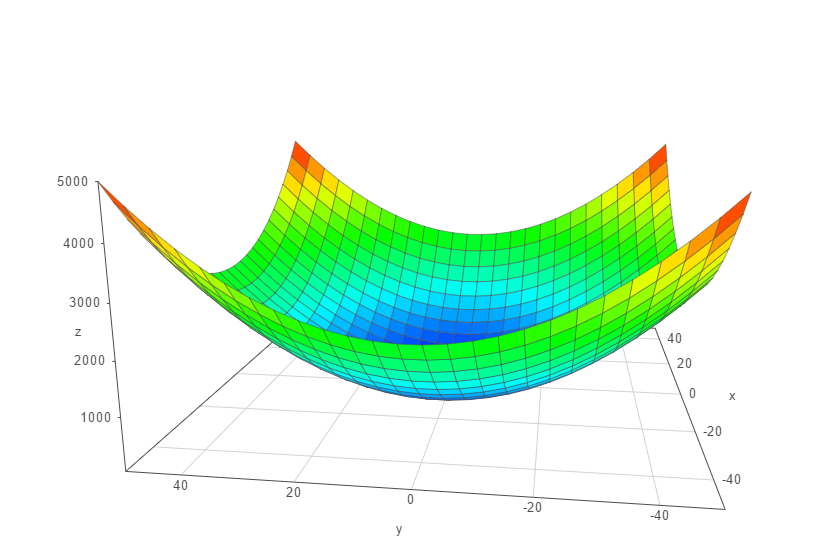
Obviously, it has extreme point (0, 0, 0). Let’s use gradient descent to get the extreme point.
Calculate the partial derivative:
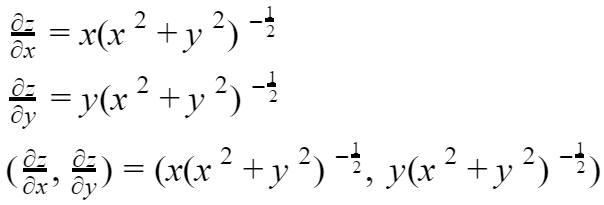
Then, let’s take any point in (x, y), and run like below. Lambda is a tiny value, which controls how fast P goes to the extreme value.
![]()
![]()
After we ran, we got the below iteration:
0 (x, y): 1.0, 5.0 1 (x, y): 0.803883864861816, 4.01941932430908 2 (x, y): 0.6077677297236319, 3.0388386486181598 3 (x, y): 0.41165159458544787, 2.0582579729272394 4 (x, y): 0.21553545944726385, 1.0776772972363193 5 (x, y): 0.019419324309079833, 0.09709662154539911 6 (x, y): -0.1766968108291043, -0.8834840541455209 7 (x, y): 0.01941932430907986, 0.09709662154539922 8 (x, y): -0.17669681082910432, -0.8834840541455209 9 (x, y): 0.01941932430907986, 0.09709662154539922 (x, y): -0.17669681082910432, -0.8834840541455209
It shows that it iterates close to the extreme value (0, 0), but it go around (0, 0) when it arrives.
My java code for this gradient descent algorithm:
public static void main (String[] args) throws java.lang.Exception{
// your code goes here
System.out.println(Math.pow((26 * 26 + 46 * 46), -0.5));
double x = 1, y = 5, delta = 1;
for (int i = 0; i < 10; i++) {
System.out.println(i + " (x, y): " + x + ", " + y);
double tmp = Math.pow((x * x + y * y), -0.5);
double x2 = x - delta * x * tmp;
double y2 = y - delta * y * tmp;
x = x2;
y = y2;
}
System.out.println("(x, y): " + x + ", " + y);
}
code on github