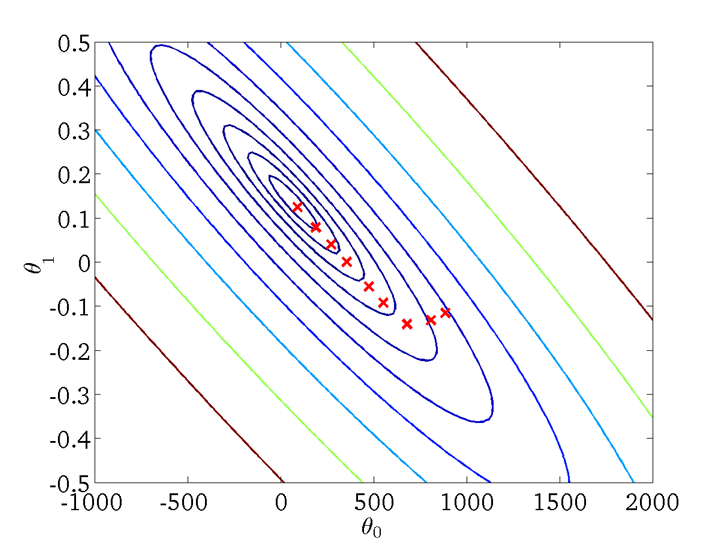
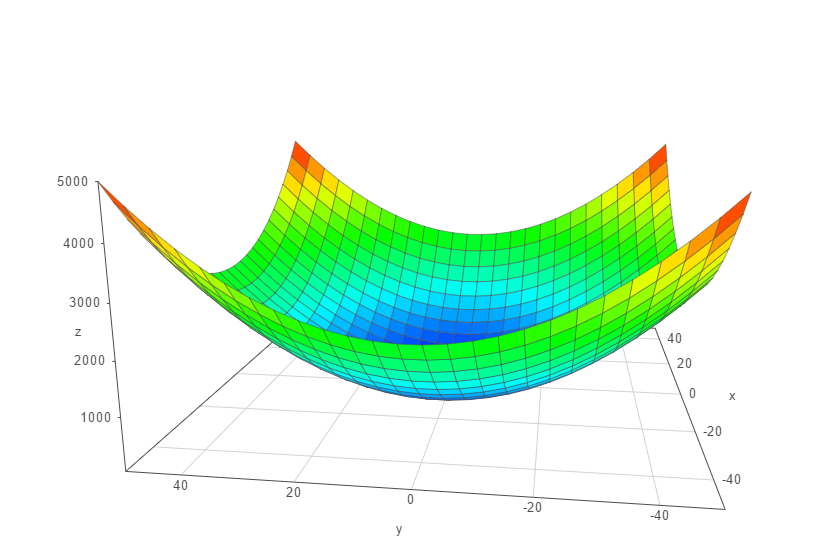
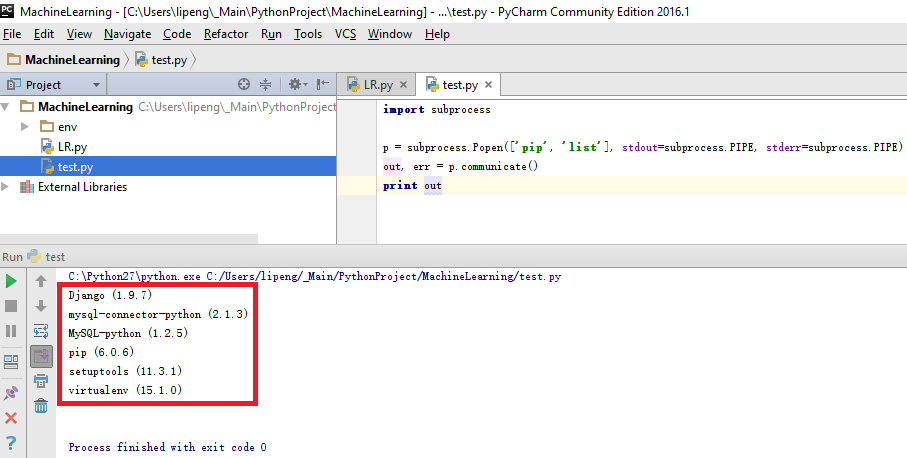
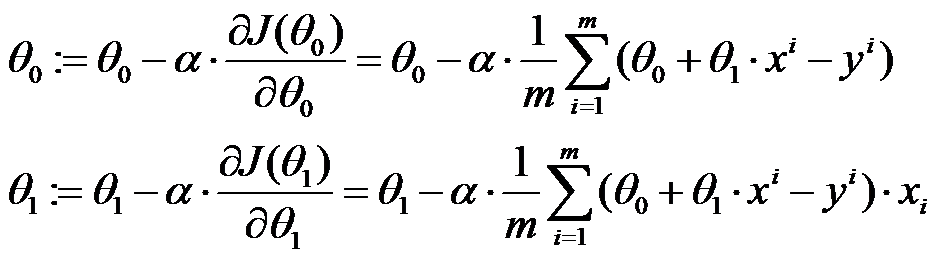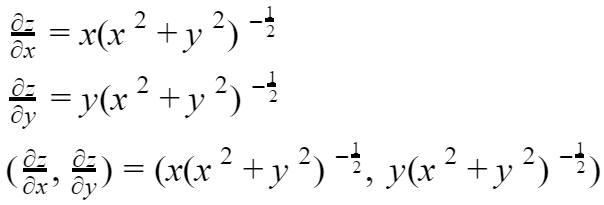Run below code, we can check what package we have under current environment.
import subprocess p = subprocess.Popen(['pip', 'list'], stdout=subprocess.PIPE, stderr=subprocess.PIPE) out, err = p.communicate() print out
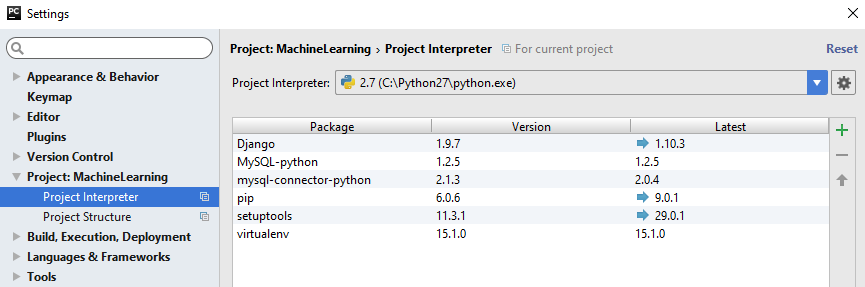
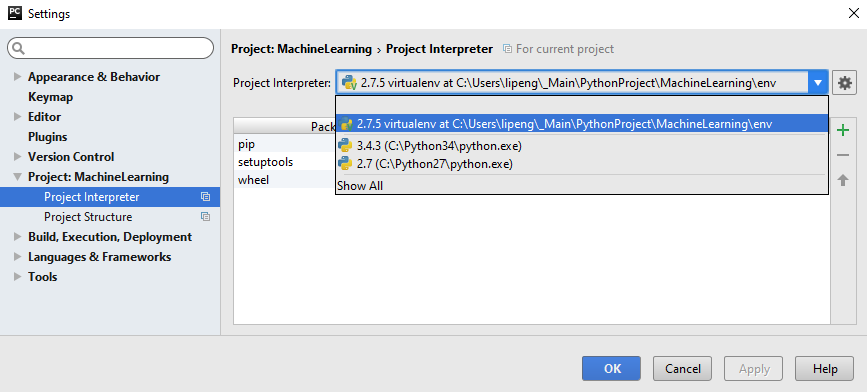
In PyCharm -> Project Interpreter -> list box Project Interpreter, here are all the python environments:
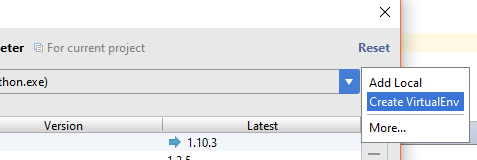
Under system button, select Create VirtualEnv
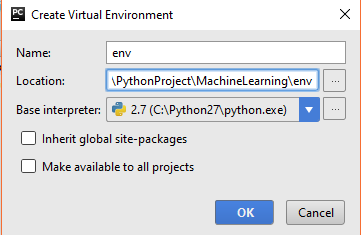
Now, we have new virtual environment.
Let’s try the code again. We see the package list changed.
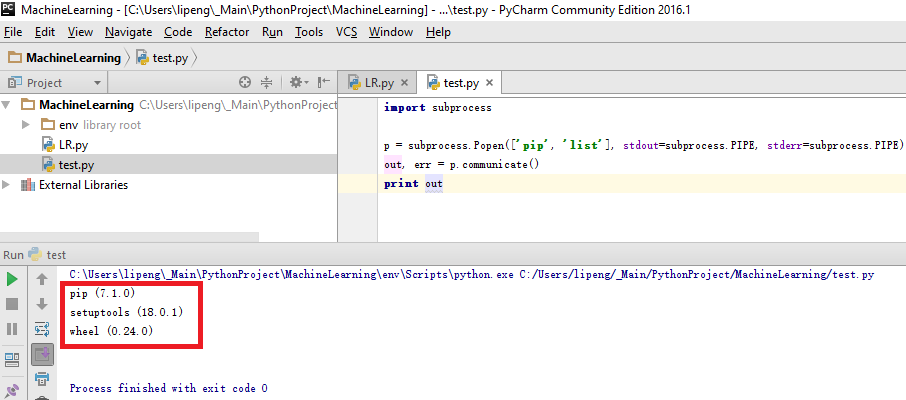
Not ended yet….
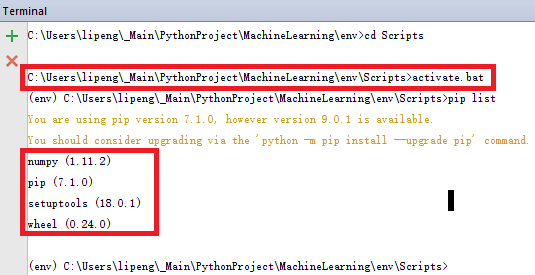
Let’s open terminal console in PyCharm and try virtualenv activate command. Unfortunately, it shows that it couldn’t find source command, which is different from Linux.
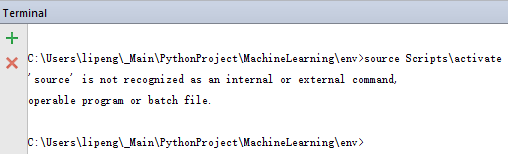
To activate virtualenv in Windows, we end up with running Scripts\activate.bat command in env folder.