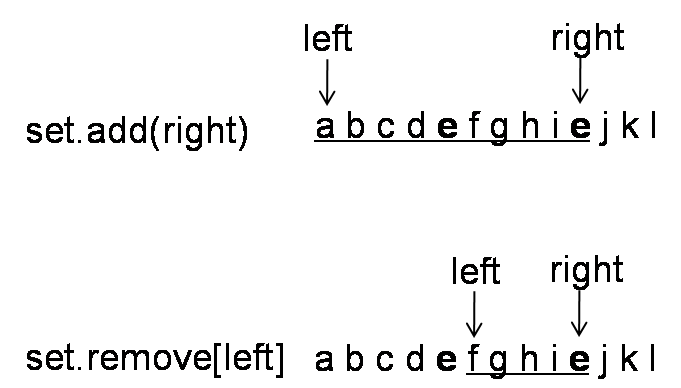Daily Archives: August 12, 2016

leetcode 15.

Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Note: The solution set must not contain duplicate triplets.

For example, given array S = [-1, 0, 1, 2, -1, -4],

A solution set is:
[
  [-1, 0, 1],
  [-1, -1, 2]
]

Solution. When the array doesn’t has duplicate, it is a classical 3Sum problem, the code is like below

public List<List<Integer>> threeSum(int[] nums) {
    Arrays.sort(nums);
    List<List<Integer>> list = new ArrayList<>();
    for (int i = 0; i < nums.length - 2; i++) {
        int left = i + 1, right = nums.length - 1;
        while (left < right) {
            int sum = nums[i] + nums[left] + nums[right];
            if (sum == 0) {
                list.add(Arrays.asList(nums[i], nums[left], nums[right]));
                left++;
                right--;
            }
            else if (sum < 0) {
                right--;
            }
            else {
                left++;
            }
        }
    }
    return list;
}

If it has duplicate, we need to skip the duplicate by several rules:
1. When iterating i, if nums[i] has same value as the previous one, nums[i] == nums[i – 1]. We need to skip
2. After we found a new pair at nums[i], nums[left] and nums[right], we need to move left forward until a different value; move right backward until a different value.

public List<List<Integer>> threeSumWithDuplicate(int[] nums) {
    Arrays.sort(nums);
    List<List<Integer>> list = new ArrayList<>();
    for (int i = 0; i < nums.length - 2; i++) {
        if (i > 0 && nums[i] == nums[i - 1]) {
            continue;
        }
        int left = i + 1, right = nums.length - 1;
        while (left < right) {
            int sum = nums[i] + nums[left] + nums[right];
            if (sum == 0) {
                list.add(Arrays.asList(nums[i], nums[left], nums[right]));
                left++;
                right--;
                while (left < right && nums[left] == nums[left - 1]) {
                    left++;
                }
                while (left < right && nums[right] == nums[right + 1]) {
                    right--;
                }
            }
            else if (sum < 0) {
                right--;
            }
            else {
                left++;
            }
        }
    }
    return list;
}

Check my code on github.

leetcode 3

Given a string, find the length of the longest substring without repeating characters.

Examples:

Given "abcabcbb", the answer is "abc", which the length is 3.

Given "bbbbb", the answer is "b", with the length of 1.

Given "pwwkew", the answer is "wke", with the length of 3. Note that the answer must be a substring, "pwke" is a subsequence and not a substring.

Solution. An awesome solution is from here. It has two pointers, left and right. s[left, right] has no duplicate.

Iterate right, if s[right] is not in HashSet, then put it in, and update ans = max(ans, right – left).

If s[right] is already in HashSet, we need to loop from left and remove s[left], until there is no s[right] in HashSet.

If the string is [a b c d e f g h i e j k l], then the process is like:

public int lengthOfLongestSubstring(String s) {
    Set<Character> set = new HashSet<>();
    int left = 0, right = 0, ans = 0;
    while (right < s.length()) {
        if (set.contains(s.charAt(right))) {    // has duplicate, move left until there is no duplicate between [left, right]
            set.remove(s.charAt(left++));
        }
        else {
            set.add(s.charAt(right++)); // has no duplicate between [left, right], move right
            ans = Math.max(ans, right - left);
        }
    }
    return ans;
}

Check my code on github.

leetcode 155.

There are many ways to solve the min stack problem. However, there is one solution which only requiring O(1) extra space.

The idea is that when pushinng, store the offset of the current min value. When pop or getTop, use the offset and min to get the top or next min.

If the [3, 4, 2, 1] enters stack sequentially, the stack looks like this:

public class MinStack {

    long min;
    Stack<Long> stack;

    public MinStack() {
        stack = new Stack<>();
    }

    public void push(int x) {
        if (stack.size() == 0) {
            min = x;
            stack.push(0l);
        }
        else {
            stack.push(x - min);
            min = Math.min(min, x);
        }
    }

    public void pop() {
        long pop = stack.pop();
        if (pop < 0) {
            min = min - pop;
        }
    }

    public int top() {
        long top = stack.peek();
        if (top < 0) {
            return (int)min;
        }
        return (int)(top + min);
    }

    public int getMin() {
        return (int)min;
    }

}

Check my code on github.