Monthly Archives: July 2016

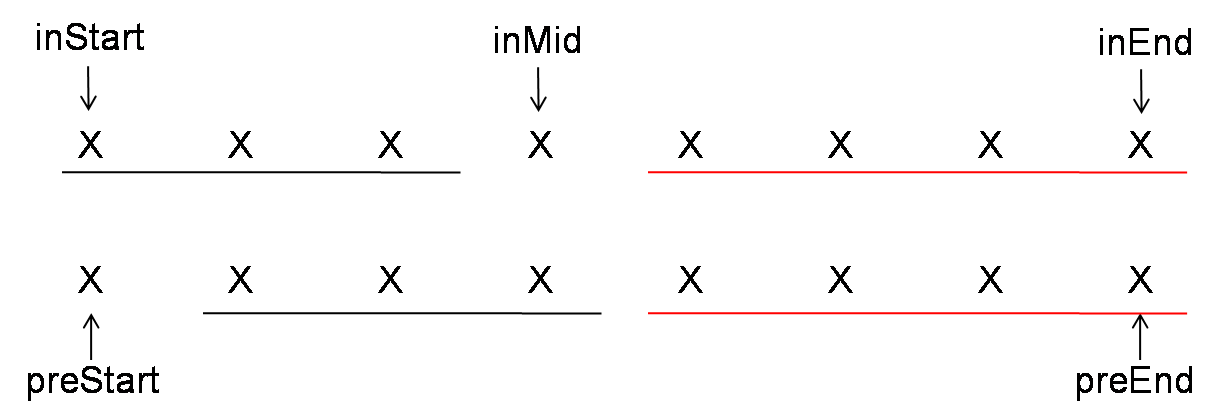
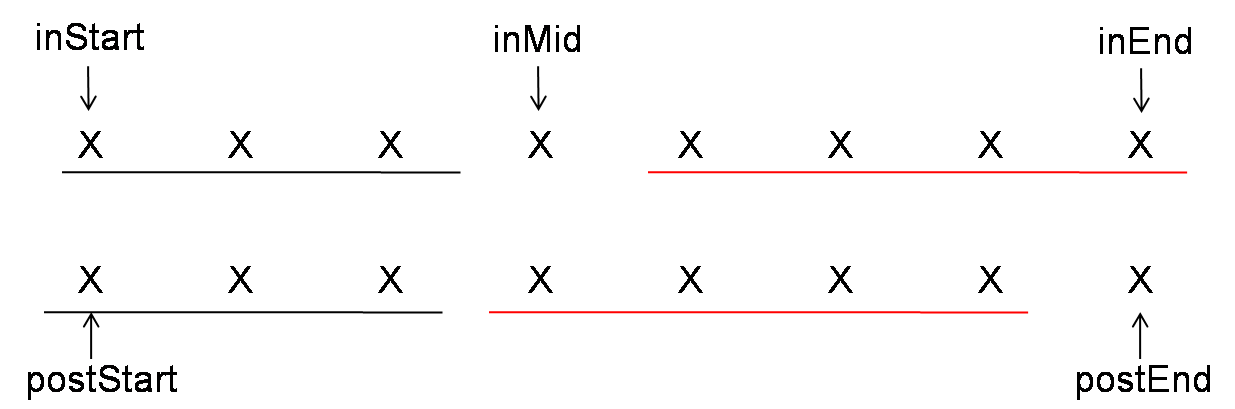
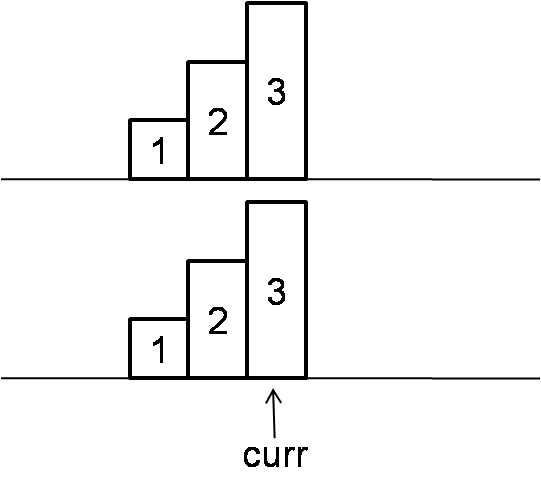
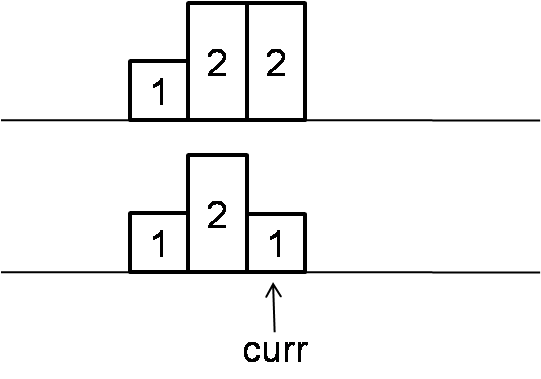
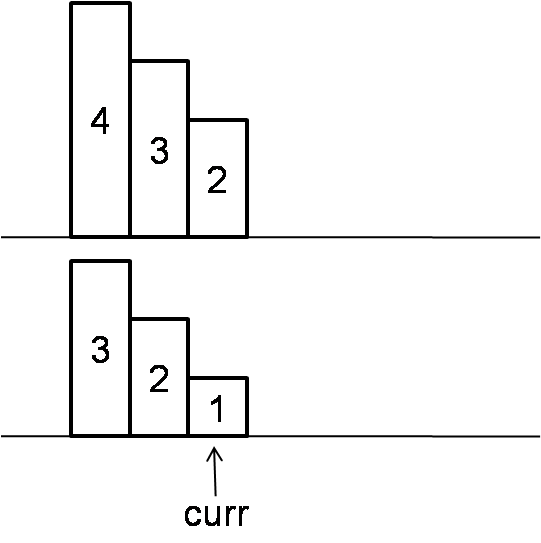
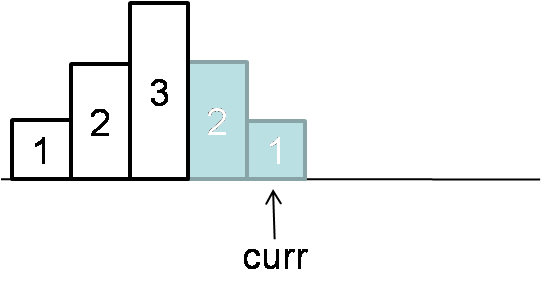
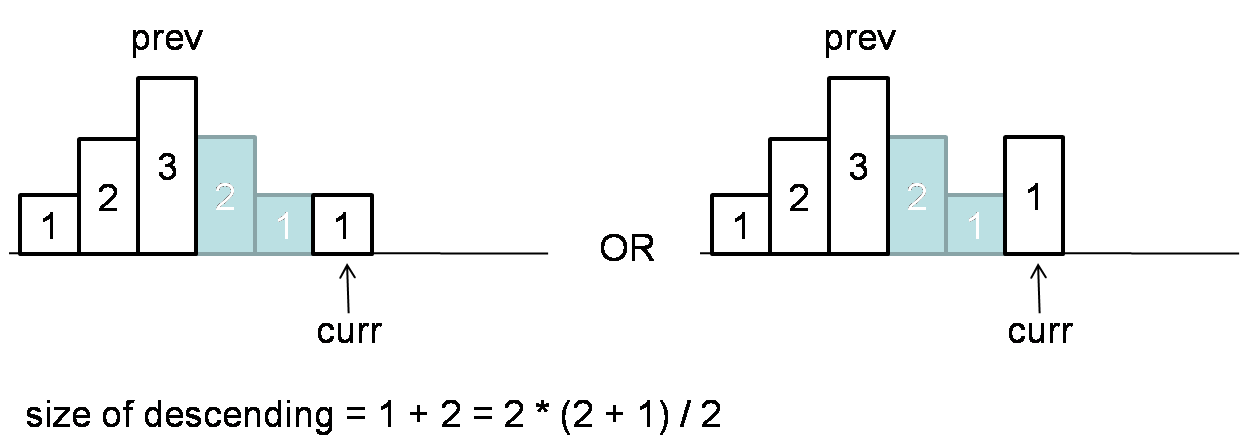
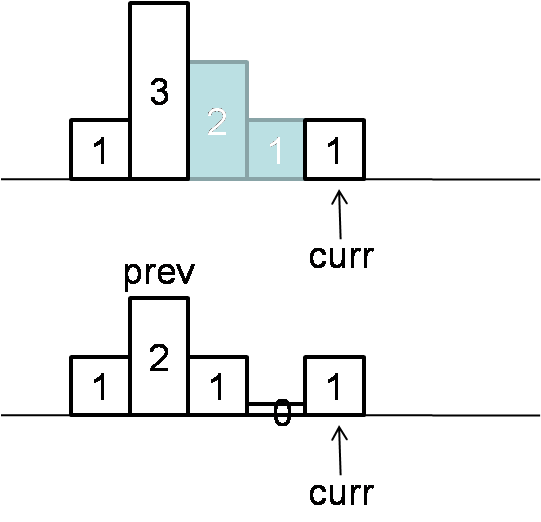Normal bst inorder traversal takes O(n) time, O(logn) space. Threaded bst inorder traversal takes O(n) time, O(1) space.

However, by Morris Traversal, we can traverse tree in O(n) time, O(1) space without constructing a threaded bst. Let me summary the rules for this algorithm.

1. If current node doesn’t has left child, then print current node. Like node 1, 3, 4, 8 etc.
   
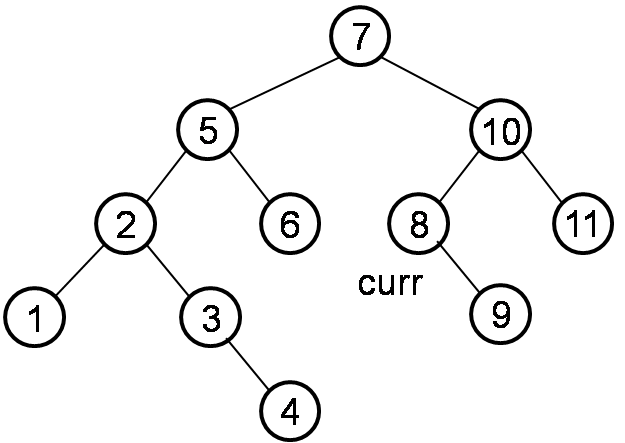
2. If current node has left child,  then we check the right-most of left child.
   2. 1 If right child of right-most  is null, then point its right child to curr.
   
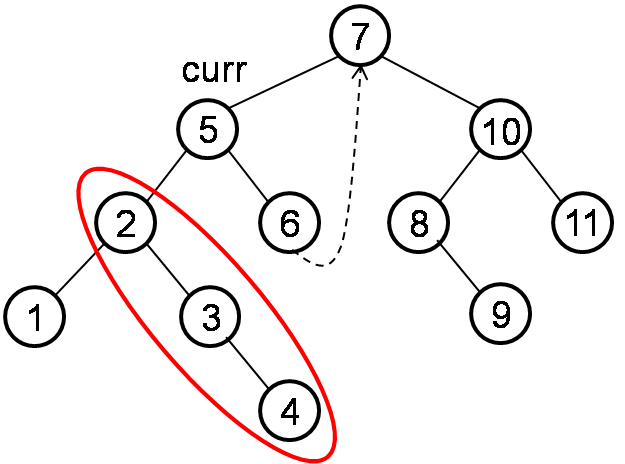
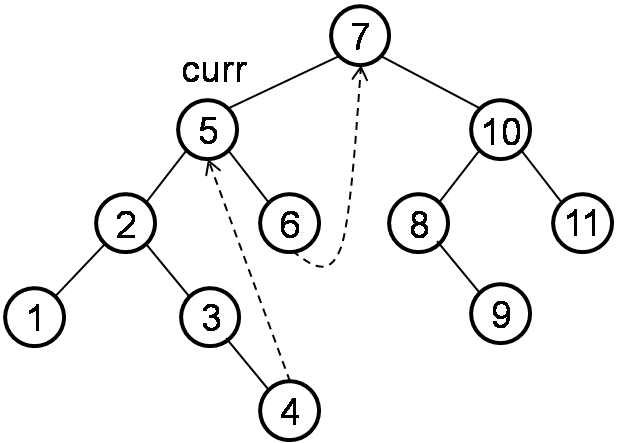
   2.2 If right child of right-most is not null, it means left child is already traversed. We need to set right child of right-most  to null.
   

This is my java code:

public static void morrisTraversal(TreeNode node) {
    TreeNode curr = node;
    while (curr != null) {
        if (curr.left == null) {    // if left is null, then print
            System.out.println(curr.val);
            curr = curr.right;
            continue;
        }
        TreeNode pre = curr.left;
        while (pre.right != null && pre.right != curr) {
            pre = pre.right;
        }
        if (pre.right == null) {
            pre.right = curr;
            curr = curr.left;
        }
        else {  // right end already points to curr, it means left is already traversed.
            pre.right = null;
            System.out.println(curr.val);
            curr = curr.right;
        }
    }   // while
}

Check my github.

leetcode 103.

Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

For example:
Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return its zigzag level order traversal as:

[
  [3],
  [20,9],
  [15,7]
]

Solution. A naive solution is to use BFS level order traversal. But the code is a bit overhead. However, there is a smart DFS solution. It checks the level. If it adds into result in sequential or reverse order based on level % 2.

This technique can also be used to solve problem like Binary Tree Level Order Traversal II

// DFS solution. Initial root level is 0.
// if level % 2 == 0, sequential order
// if level % 2 == 1, reverse order
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
    List<List<Integer>> ans = new ArrayList<>();
    zigzagHelper(root, ans, 0);
    return ans;
}

private void zigzagHelper(TreeNode root, List<List<Integer>> ans, int level) {
    if (root == null) {
        return;
    }
    if (level >= ans.size()) {
        ans.add(new LinkedList<>());
    }
    LinkedList<Integer> curr = (LinkedList)ans.get(level);
    if (level % 2 == 0) {
        curr.addLast(root.val);
    }
    else {
        curr.addFirst(root.val);
    }
    zigzagHelper(root.left, ans, level + 1);
    zigzagHelper(root.right, ans, level + 1);
}

Check my code on github.

leetcode 105, 106.

Given preorder and inorder traversal of a tree, construct the binary tree.

Given inorder and postorder traversal of a tree, construct the binary tree.

Solution. These two are classical tree problem in data structure class.

For preorder-inorder, the process is like below:

For inorder-postorder, the process is like below:

When we have preorder[preStart], and we want to find inMid. One technique is that we store the inorder[pos] and pos in hashmap. In this way, we can find the inMid in O(1) time.

Preorder-inorder:

public static TreeNode buildTree(int[] preorder, int[] inorder) {
    if (inorder == null) {
        return null;
    }
    HashMap<Integer, Integer> hm = new HashMap<>();
    for (int i = 0; i < inorder.length; i++) {
        hm.put(inorder[i], i);
    }
    return helper(inorder, preorder, 0, inorder.length - 1, 0, preorder.length - 1, hm);
}

private static TreeNode helper(int[] inorder, int[] preorder, int inStart, int inEnd, int preStart, int preEnd, HashMap<Integer, Integer> hm) {
    if (inStart > inEnd) {
        return null;
    }
    int inMid = hm.get(preorder[preStart]);
    TreeNode node = new TreeNode(inorder[inMid]);
    node.left = helper(inorder, preorder, inStart, inMid - 1, preStart + 1, preStart + inMid - inStart, hm);
    node.right = helper(inorder, preorder, inMid + 1, inEnd, preStart + inMid - inStart + 1, preEnd, hm);
    return node;
}

Inorder-postorder:

public static TreeNode buildTree(int[] inorder, int[] postorder) {
    if (inorder == null) {
        return null;
    }
    HashMap<Integer, Integer> hm = new HashMap<>();
    for (int i = 0; i < inorder.length; i++) {
        hm.put(inorder[0], i);
    }
    return helper(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1, hm);
}

private static TreeNode helper(int[] inorder, int[] postorder, int inStart, int inEnd, int postStart, int postEnd, HashMap<Integer, Integer> hm) {
    if (inStart > inEnd) {
        return null;
    }
    int inMid = hm.get(postorder[postEnd]);
    TreeNode node = new TreeNode(inorder[inMid]);
    node.left = helper(inorder, postorder, inStart, inMid - 1, postStart, postEnd - (inEnd - inMid) - 1, hm);
    node.right = helper(inorder, postorder, inMid + 1, inEnd, postEnd - (inEnd - inMid), postEnd - 1, hm);
    return node;
}

Check my code on github: preorder-inorder, inorder-postorder.

leetcode 109

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

Solution. At the beginning, I came up idea to use slow and fast point to find the middle element, and generate node. And recursively do left and right side. But this takes O(nlogn) time.

// O(nlogn) solution
public static TreeNode sortedListToBST2(ListNode head) {
    if (head == null) {
        return null;
    }
    if (head.next == null) {
        return new TreeNode(head.val);
    }
    ListNode slow = head, fast = head.next; // pivot should be slow.next. In this way, it is easy to set slow.next = null
    while (fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    TreeNode node = new TreeNode(slow.next.val);    // pivot is slow.next
    ListNode next = slow.next.next;
    slow.next = null; // cut the list.
    node.left = sortedListToBST2(head);
    node.right = sortedListToBST2(next);
    return node;
}

However, there is a better O(n) solution. First, count the number of ListNode. And build the AVL tree based on the number.

For 1, 2, 3, 4, 5, 6. mid = 4, left = [1, 2, 3], right = [5, 6]
For 1, 2, 3, 4, 5, 6, 7. mid = 4, left = [1, 2, 3], right = [5, 6, 7]

The code is like below:

// O(n) time, O(logN) solution.
// count number of ListNode, then divide n into 3 parts. And recursively build the AVL tree
// for 1, 2, 3, 4, 5, 6. mid = 4, left = [1, 2, 3], right = [5, 6]
// for 1, 2, 3, 4, 5, 6, 7. mid = 4, left = [1, 2, 3], right = [5, 6, 7]
private ListNode head = null;

public TreeNode sortedListToBST(ListNode head) {
    this.head = head;
    int n = 0;
    ListNode node = head;
    while (node != null) {
        n++;
        node = node.next;
    }
    return helper(n);
}

private TreeNode helper(int n) {
    if (n <= 0) {
        return null;
    }
    int mid = n >> 1;
    TreeNode left = helper(mid);    // left part
    TreeNode node = new TreeNode(head.val);
    head = head.next;
    node.left = left;
    node.right = helper(n - mid - 1);   // right part
    return node;
}

Check my code on github.

leetcode 114.

Given a binary tree, flatten it to a linked list in-place.

For example,
Given

         1
        / \
       2   5
      / \   \
     3   4   6

The flattened tree should look like:

   1
    \
     2
      \
       3
        \
         4
          \
           5
            \
             6

Solution. I learned the solution from here. The point is that build a helper(TreeNode node) function. The helper function will not only flatten node, but also return the tail of the flattened list.

After traverse left and right node, we have leftTail, rightTail and root. We can reconstruct the flatten list easily.

public static void flatten(TreeNode root) {
    helper(root);
}

public static TreeNode helper(TreeNode root) {
    if (root == null) {
        return null;
    }
    TreeNode leftTail = helper(root.left);
    TreeNode rightTail = helper(root.right);
    if (leftTail != null) {
        leftTail.right = root.right;
        root.right = root.left;
        root.left = null;
    }
    if (rightTail != null) {
        return rightTail;
    }
    if (leftTail != null) {
        return leftTail;
    }
    return root;
}

Check my code on github.

leetcode 132

Given a string s, partition s such that every substring of the partition is a palindrome.

Return the minimum cuts needed for a palindrome partitioning of s.

For example, given s = "aab",
Return 1 since the palindrome partitioning ["aa","b"] could be produced using 1 cut.

Solution. At the beginning, I tried to use DFS and recursion way. But both of them got TLE. This problem is actually can be solved in O(n^2) time. I learned from here.

This can be treated as 1-dimension dp problem. Let’s define array cut[]. cut[j] is the minimum cut of s[0…j]. Ok, then we can calculate cut[j] from cut[j – 1]. Let’s say the position i before j. If s[i…j] is palindrome, the cut[j] = min{cut[[j], cut[i – 1] + 1}.

Like below one, cut[6] = min{cut[6], cut[2] + 1}.

In order to check if s[i…j] is palindrome. We need a boolean dp[][] array, can check if s[i] == s[j] and d[[i + 1…j – 1] == true.

// dp solution. O(n^2) time complexity
public static int minCut(String s) {
    boolean[][] dp = new boolean[s.length()][s.length()];
    int[] cut = new int[s.length()];
    Arrays.fill(cut, Integer.MAX_VALUE);
    for (int j = 0; j < cut.length; j++) {
        for (int i = 0; i <= j; i++) {
            // check dp[i][j]. when i + 1 >= j this is for checking length less than or eqaul to 2. such as 'a', 'ab'
            dp[i][j] = s.charAt(i) == s.charAt(j) && (i + 1 >= j || dp[i + 1][j - 1]);
            if (dp[i][j]) {
                // when i == 0, it means whole s[0...j] is a palindrome.
                cut[j] = Math.min(cut[j], i == 0 ? 0 : cut[i - 1] + 1);
            }
        }
    }
    return cut[dp.length - 1];
}

Check my code on github.

leetcode 133.

Clone an undirected graph. Each node in the graph contains a label and a list of its neighbors.

       1
      / \
     /   \
    0 --- 2
         / \
         \_/

public static UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
    return clone(node, new HashMap<>());
}

private static UndirectedGraphNode clone(UndirectedGraphNode node, HashMap<Integer, UndirectedGraphNode> hm) {
    if (node == null) {
        return null;
    }
    if (hm.containsKey(node.label)) {
        return hm.get(node.label);
    }
    UndirectedGraphNode cloneNode = new UndirectedGraphNode(node.label);
    hm.put(cloneNode.label, cloneNode);
    for (UndirectedGraphNode neighbor : node.neighbors) {
        cloneNode.neighbors.add(clone(neighbor, hm));
    }
    return cloneNode;
}

Check my code on github.

There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station’s index if you can travel around the circuit once, otherwise return -1.

Solution.

We set diff[i] = gas[i] – cost[i]. First of all, there is always a result if total sum of diff is greater than 0, or there won’t be a result.

Consider below cases:

gas[]  = [3,  2,  0, 0,   1,  2,  2]
cost[] = [2,  1,  1,  1,   2,  3,  0]
diff[] =  [1,  1, -1, -1, -1, -1,  2]

Let’s consider about diff[]. Basically, we need to find a point i in diff. And starting from this point i, move after it and count sum[diff[i], … ]. In this process, any j which is “behind” i should have sum[diff[i], …, diff[j]] >= 0. 

We have this assumption for point i: if j is the first element “behind” i which makes sum[diff[i], …, diff[j]] < 0, then any element between (i, j) has sum[diff[i], …, diff[k]] < 0.

Let’s do a rough assumption by using a line. j is the first element after i, which makes sum[i….j] < 0. So we have sum[i…j] < 0, sum[i…k] >= 0

Besides we know sum[i…j] = sum[i…k] + sum[k…j]. So we can conclude that sum[k…j] < 0.

Once we know this, we just do the sum of diff. Whenever the sum is less than zero, we set target to next element. Until we find an element which makes the sum is greater than 0 toward the end.

public int canCompleteCircuit(int[] gas, int[] cost) {
    // test see if there is a result.
    int total = 0;
    for (int i = 0; i < gas.length; i++) {
        total += gas[i] - cost[i];
    }
    if (total < 0) {
        return -1;
    }
    // calculate the aggregation until we find a position which the aggregation from it to the end is greater than or equal to 0
    int aggr = 0, ans = 0;
    for (int i = 0; i < gas.length; i++) {
        aggr += gas[i] - cost[i];
        if (aggr < 0) {
            ans = i + 1;
            aggr = 0;
        }
    }
    return ans;
}

Check my code on github.

leetcode 135.

There are N children standing in a line. Each child is assigned a rating value.

You are giving candies to these children subjected to the following requirements:

• Each child must have at least one candy.
• Children with a higher rating get more candies than their neighbors.

What is the minimum candies you must give?

Solution. This problem can be easily solved by scanning the array from left to right, right to left in O(n) time and O(n) space.

But there is a O(n) time, O(1) space solution, which is pretty hard to understand. Let me try to explain this O(1) space solution.

If current rating is greater than previous one, then current value should be prev + 1

If current rating is equal to previous one, then current value should be 1

If current rating is less than previous one, we don’t know the value yet.

Let’s consider the continuous descending ratings. If there is continuous descending ratings, we will use countDown to memorize the descending length. Below case, countDown = 2 at curr position.

During a descending order, when curr is equal to previous or greater than previous, we can use progression formula to calculate the descending area size.

Let’s reconsider the prev when calculating size of descending area. Think about below case. Prev is 2, which is not tall enough and makes next 2 elements to 1 and 0.

In this case when countDown >= prev, we should increase prev by countDown – prev + 1.

The final code is like below:

public static int candy(int[] ratings) {
    int pre = 1, countDown = 0, total = 1;
    for (int i = 1; i < ratings.length; i++) {
        if (ratings[i] >= ratings[i - 1]) {
            if (countDown > 0) {
                total += countDown * (countDown + 1) / 2;   // progression part
                if (countDown >= pre) { // check if pre is tall enough
                    total += countDown - pre + 1;
                }
                pre = 1;    // when ascending and there is countDown, prev should be 1
                countDown = 0;
            }
            pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;   // when equals to previous one, set to 1. Else set to prev + 1
            total += pre;
        }
        else {
            countDown++;
        }
    }
    if (countDown > 0) {    // check if there is countDown in the end
        total += countDown * (countDown + 1) / 2;
        if (countDown >= pre) {
            total += countDown - pre + 1;
        }
    }
    return total;
}

Check my code on github.

leetcode 137.

Given an array of integers, every element appears three times except for one. Find that single one.

Solution. For example, if the numbers are [5, 5, 5, 2, 2, 2, 3]. We count the sum of 1 in each bit among these number. If the sum % 3 == 0, it means the answer should be 0 for this bit. Or it should be 1.

I don’t quite understand the best solution in discussion. But I think this solution is durable and easy to understand.

public static int singleNumber(int[] nums) {
    int ans = 0;
    for (int i = 0; i < 32; i++) {
        int sum = 0, bit = 1 << i, base = 1 << i;
        for (int j = 0; j < nums.length; j++) {
            if ((nums[j] & bit) != 0) {
                sum++;
            }
        }
        if (sum % 3 != 0) {
            ans = ans | base;
        }
    }
    return ans;
}

Check my code on github.