Monthly Archives: January 2016

Zigzag Iterator

This question is from leetcode zigzag iterator.

Given two 1d vectors, implement an iterator to return their elements alternately.

For example, given two 1d vectors:

v1 = [1, 2]
v2 = [3, 4, 5, 6]
By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: [1, 3, 2, 4, 5, 6].

First solution I gave out only work for 2 lists. I use currItr to indicate the current work iterator.

Second solution is used by a queue or linkedlist for iterators. It works for Zigzag for k iterators. It should guarantee that each iterator in queue’s hasNext() returns true. Then it pop the next value from the tail iterator, and return the value. Add the tail iterator to head if it still hasNext() is true.

check my code on github: solution1, solution2

Move Zero

This one is from leetcode which I think is very useful. https://leetcode.com/problems/move-zeroes/

Given an array nums, write a function to move all 0‘s to the end of it while maintaining the relative order of the non-zero elements.

For example, given nums = [0, 1, 0, 3, 12], after calling your function, nums should be [1, 3, 12, 0, 0].

A straight-forward solution is similar to insertion sort, which come up O(N^2) time complexity. However, here is a O(N) solution. The solution is that we make the non-zero elements to the left half. Then we put 0 to the rest.

The code is pretty neat, only with several lines.

Check my code on github: link

Peeking Iterator

https://leetcode.com/problems/peeking-iterator/

Given an Iterator class interface with methods: next() and hasNext(), design and implement a PeekingIterator that support the peek() operation — it essentially peek() at the element that will be returned by the next call to next().

Here is an example. Assume that the iterator is initialized to the beginning of the list: [1, 2, 3].

Call next() gets you 1, the first element in the list.

Now you call peek() and it returns 2, the next element. Calling next() after that still return 2.

You call next() the final time and it returns 3, the last element. Calling hasNext() after that should return false.

Solution
The solution is that we still use normal iterator. But we define a peek variable. Before next() is called, we already got the iterator.next() in peek. When peek() function is called, we just return peek. For hasNext() function, we return true if peek is not null;

check my code on github: link

Summaries for Game Theory

I came across some problem regarding game theory. I studied for a little bit. Here are some of my summaries. Even though it is still superficial.

Impartial Game: In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric. In other words, the only difference between player 1 and player 2 is that player 1 goes first.

Normal Play: The player who takes the last move wins.

Misere Play: The player who takes the last move loose.

In a normal play impartial game, we define P are the positions where previous player can win; N is the position where the next player can win. From P, it can only reach N state. From N, it can reach either N or P state. P is like a balanced position:
gt1

For most of a problem, we are asked if there is a MUST-WIN strategy for a given state.

Assume A is a set of integers. mex(A) is minimum integer number(greater than or equal to 0) which doesn’t appear in set A. g(x) = mex{g(y) : y ∈ F(x)}

For example, mex({2,4,5,6}) = 0, mex({0,1,2,6}) = 3. Consider a state graph like below:
gt4
We can get the g(x) for each point:
gt5
We can know that the point with value 0 are the P points.

For example, in Subtraction Game, we have a pile of stones. And each time, a player can only remove 1, 3 or 4 stones. The player who get the rest is the winner. In this game, it has N, P position like below:

0 1  2  3  4  5  6  7  8  9  10  11  12  13  14

0 1  0  1  2  3  2  0  1  0   1    2    3    2    0     <— mex values

P N P  N N N  N P N  P  N   N   N    N   P

Nim game is that there are n piles of stone. Each player can take any number of stones from each pile. When n = 2, a set of state graph is like below:
gt2

We can see the P position are marked red. We see it is a P position if it complies formula gt3

Wythoff’s Game. There are 2 piles of stones. A player either take same amount of stones from 2 piles, or any number of stones from one pile. It has below solution:
gt6

Sample points are like: (1,2), (3,5), (4,7), (6,10), (8,13), (9,15), …
Besides, golden cut rate has a beautiful formula: gt7

Here are some nice articles for game theory:
http://web.mit.edu/sp.268/www/nim.pdf
https://math.mit.edu/research/highschool/primes/materials/2014/conf/12-2-Xiong.pdf
https://www.youtube.com/watch?v=iyA6y6PKiC4

Binary Indexed Tree

https://leetcode.com/problems/range-sum-query-mutable/

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

This problem can be surely solved by segment tree. However, another approach is to use binary indexed tree. Binary indexed tree also provides O(logN) time for lookup, O(logN) update. But it is easier to implement and takes O(N) storage.

Let’s start by talking about a bit operation. For example, if we have a = 00110100 in binary, and we want to get the as much as zero from right until it reaches the 1st 1, which is 100. We can do (-a) & a. It is because in machine, all number uses complement form. It has below calculation:
complement of a:   00110100
complement of -a:  11001100
So (-a) & a = 100

Let’s see an example of binary indexed tree for index 1 to 15. Assume we built an binary indexed tree for nums[] array.
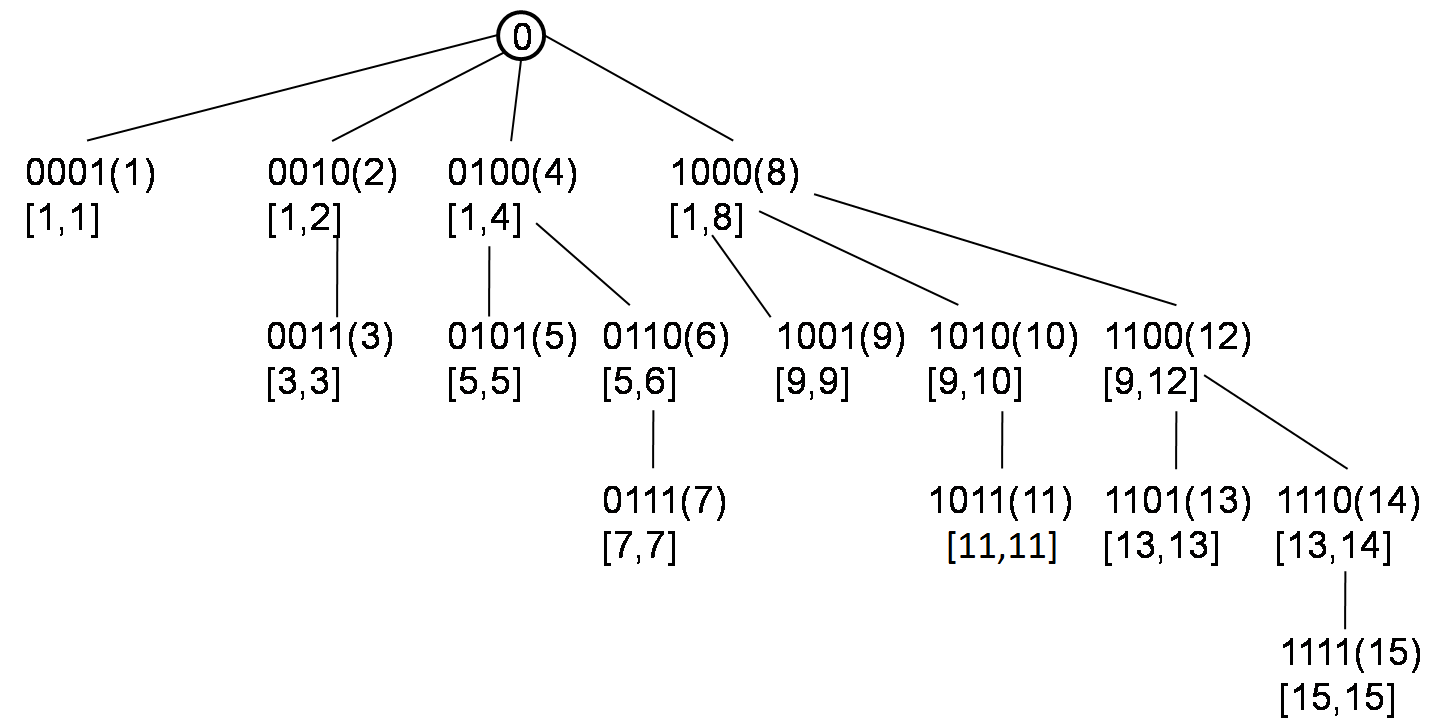
binaryindexedtree2
In this tree structure, take 1011(11) as example. The value of tree[11] contains nums[11]. In order to get the rangeSum(1, 11), we just add value of its ancestry: tree[11] + tree[10] + tree[8].

tree[10] contains nums[9], nums[10]; tree[8] contains value nums[1], nums[2], nums[3],…,nums[8].

rangeSum(1, 11) = tree[1011] + tree[1010] + tree[1000].

Another example, rangeSum(1, 7) = tree[0111] + tree[0110] + tree[0100]

So, we can find the rule for sum:

while (idx > 0) {
    sum += tree[idx];
    idx -= (-idx) & idx;
}

Let’s talk about how do we updat. Let’s say we increase 2 to nums[5]. Then we should increase 2 to tree[0101], tree[0110], tree[1000]. Another example, we want to add 2 to nums[9], then we need to add 2 to tree[1001], tree[1010], tree[1000]. So we can find the rule for increase a value to nums[idx]:

while (idx <= n) {
    tree[idx] += val;
    idx += (-idx) & idx;
}

check my code on github: link

Segment tree, lazy propagation

Segment tree is a very useful data structure which can give answer for range problem in O(logN) time once we have pre-built the tree. Such as sum, min, max in range [i, j]. Lazy propagation is used to lazily update value in segment tree. We try not to update node value as much as possible. We only update in a HAVE-TO situation.

In order to build SegmentTree, we need a Node structure to fill up the tree. A typical Node structure is like below:

private class Node {

    int value;  // value indicates the position in nodes[] array
    int from;   // from and to is the range of node
    int to; // from and to is the range of node
    int size;   // range length of node
    int min;
    int sum;

    /*When pendingVal is null, means no pendingVal. Otherwise it is the pending value.
    Pending value is used to propagate node's children.
    When update pending value, min and sum are both update too. */
    Integer pendingVal;
}

There are several useful function for segment tree.

contains(from1, to1, from2, to2)  // to tell is range1 includes range2

overlap(from1, to1, from2, to2)  // return true too if contains

update(from, to, value)  // add value to element in range[from,…,to]

Pending value in Node structure is a important one for lazy propagation. When update or query a node for a range, if node contains the range, we just update or return value. If node is a leaf node, we return. Or if node overlap with range, then we should proceed to node’s children nodes. Before we proceed to children nodes, we need to propagate the children nodes by the pending value in node.

When we propagate the node on its children, we simply return if pending value is null. If pending value from parent node is not null, we update children’s pending value and update children’s sum/min. After propagate, we set pending value of parent node to null. In each status of a node, as long as a node has pending value, we should make sure the node’s sum/min value is already updated.

Let’s try a process for below case,
seg1
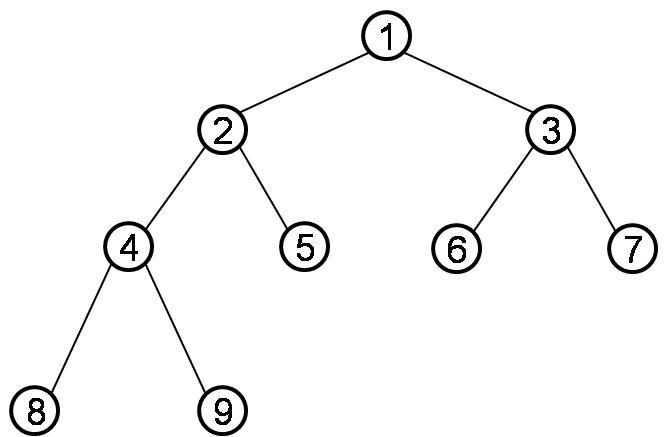
num[] = [1, 2, 3, 4, 5]
update(0, 2, 1);  [2, 3, 4, 4, 5]
update(0, 2, 1);  [3, 4, 5, 4, 5]
update(1, 1, 1);  [3, 5, 5, 4, 5]
update(3, 4, 1);  [3, 5, 5, 5, 6]
querySum(2, 3);  return 10

The process is like below:
seg2
seg3
seg4
seg5
seg6
seg7
seg8
seg9

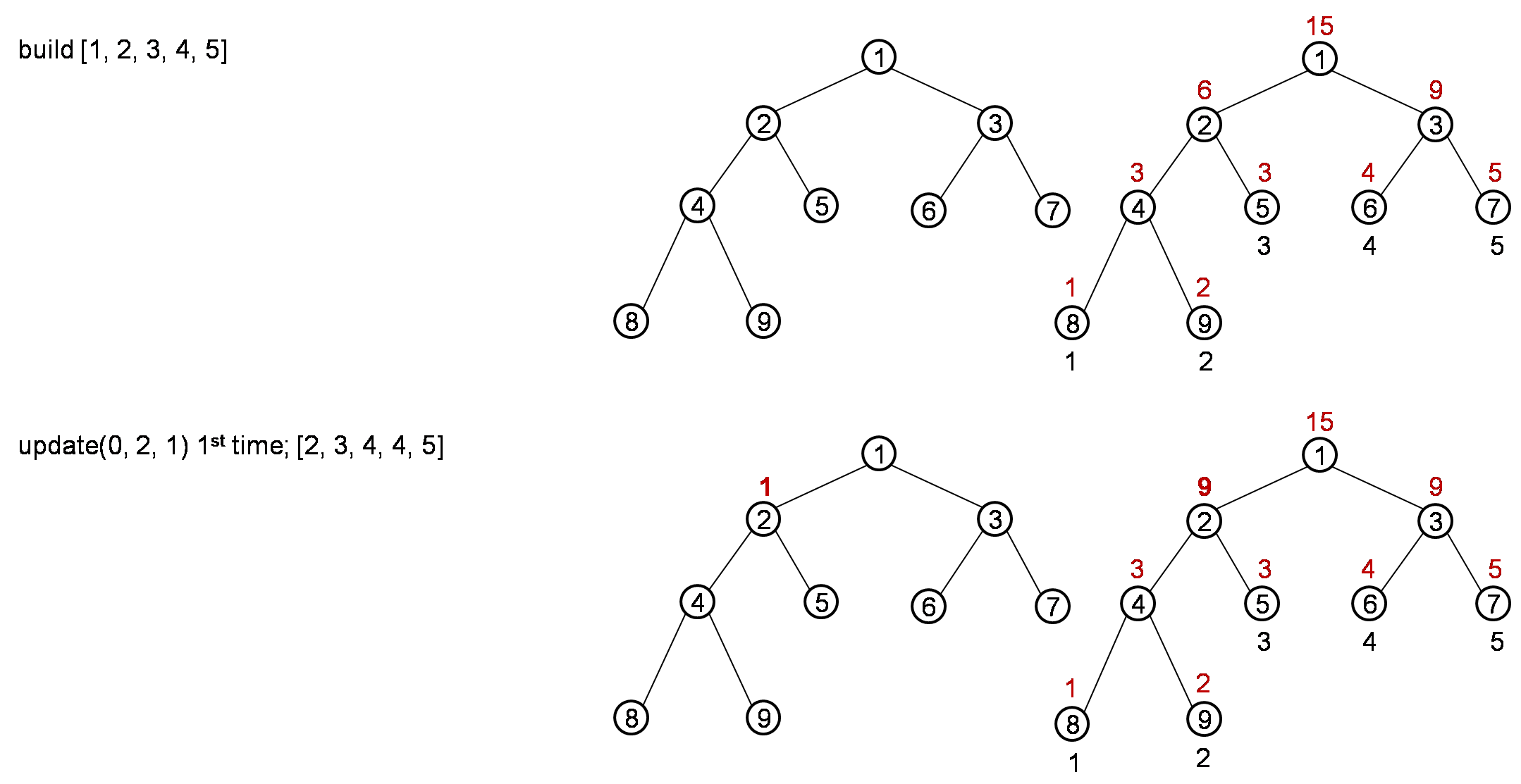
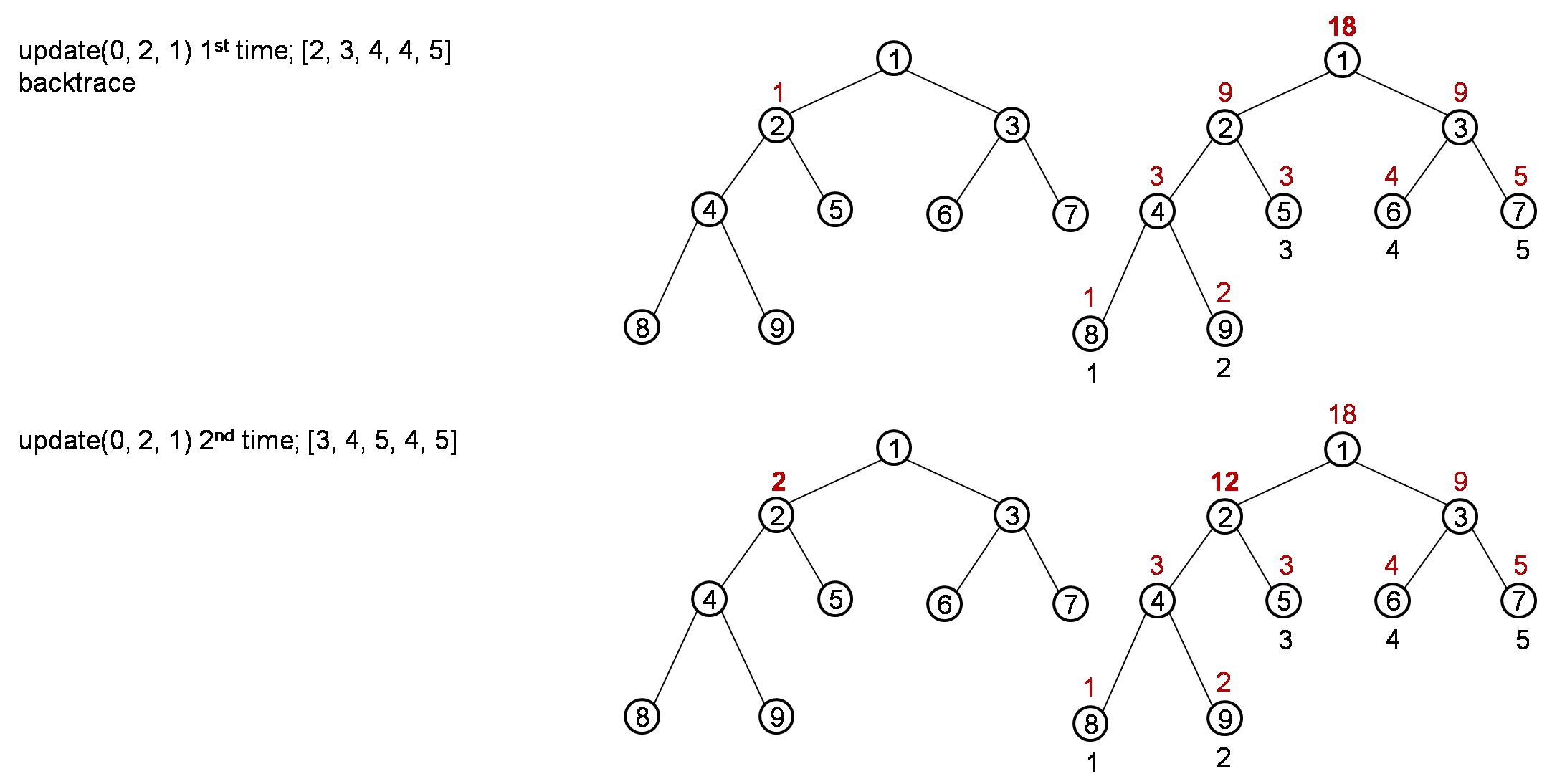
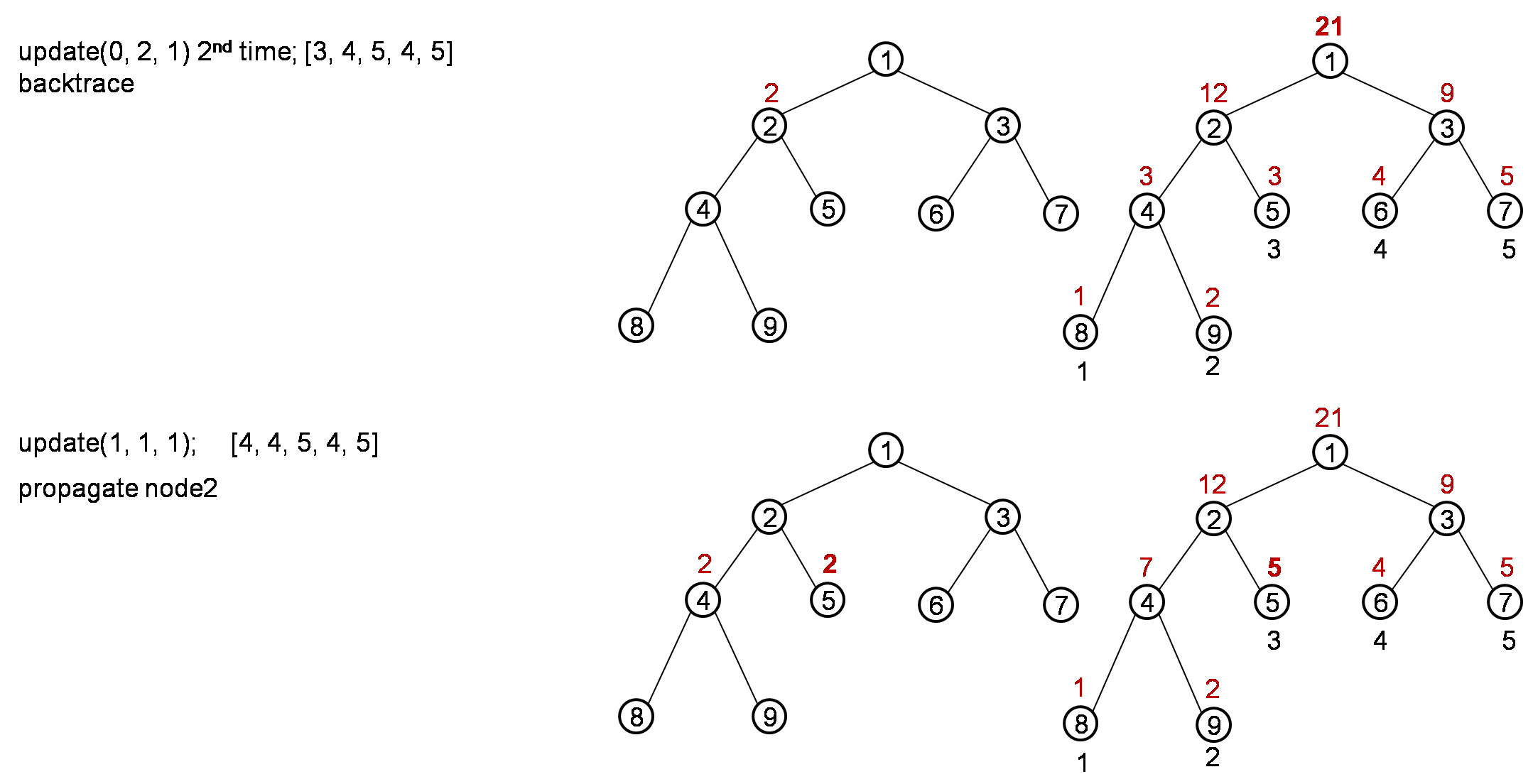
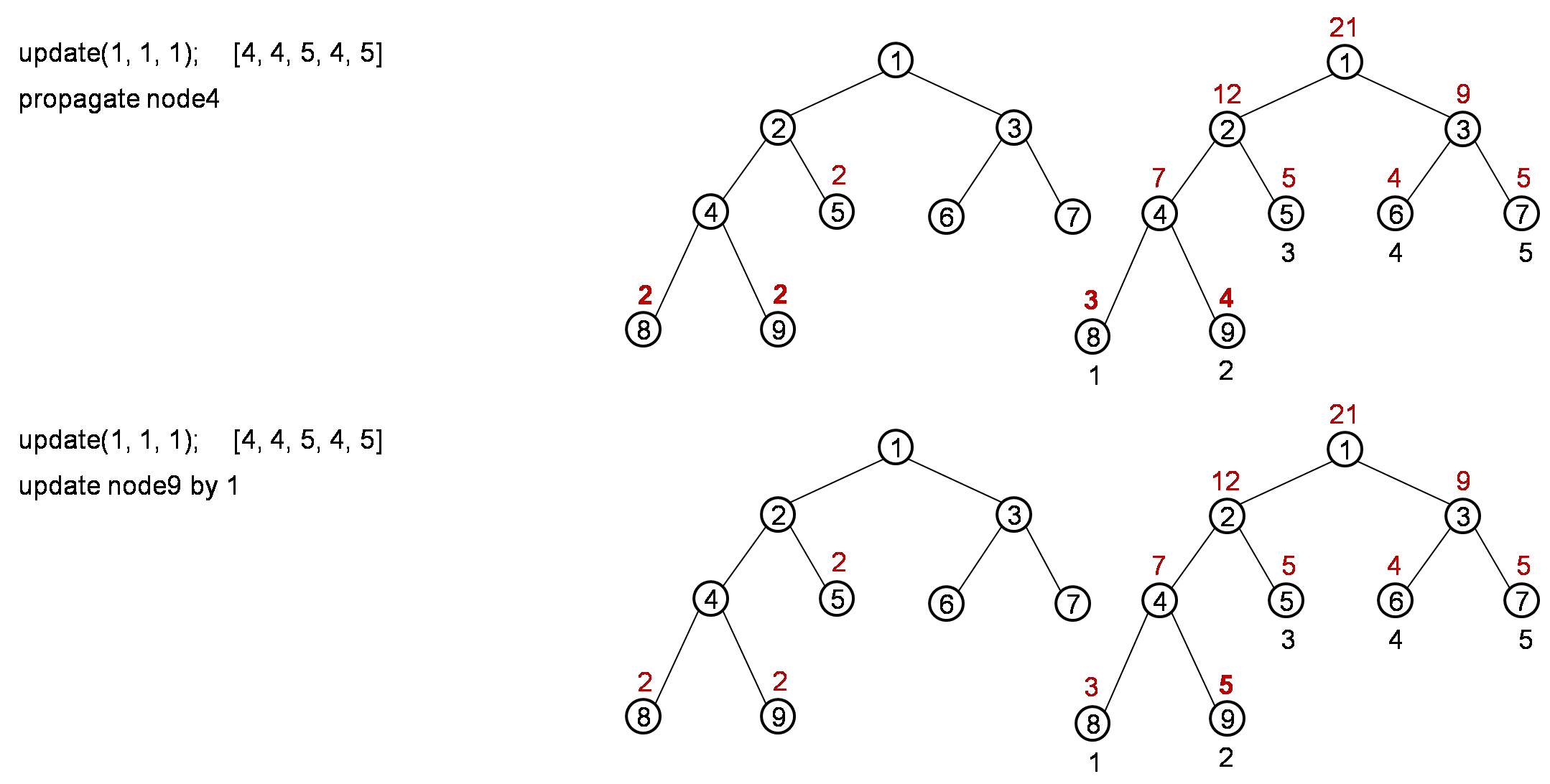
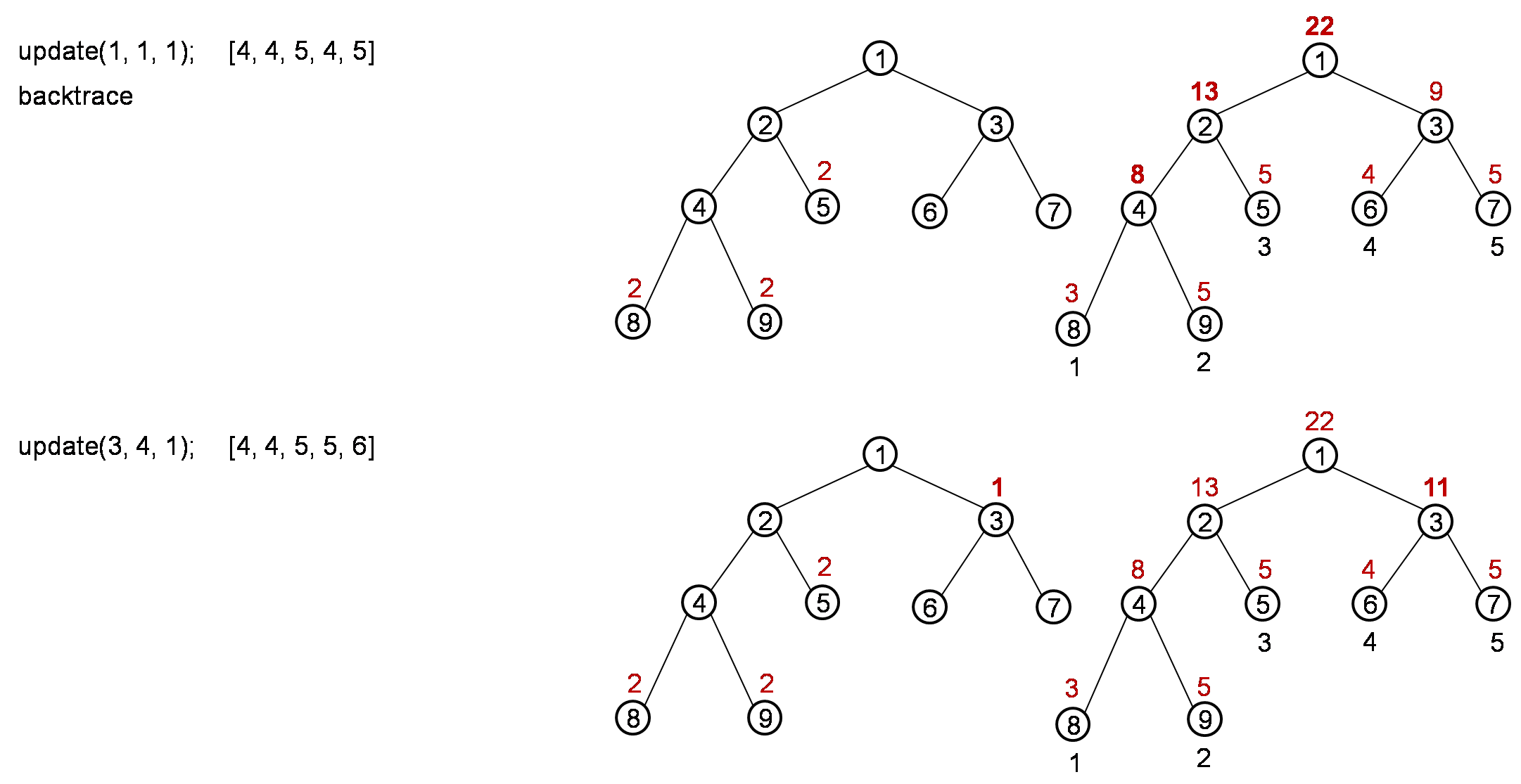
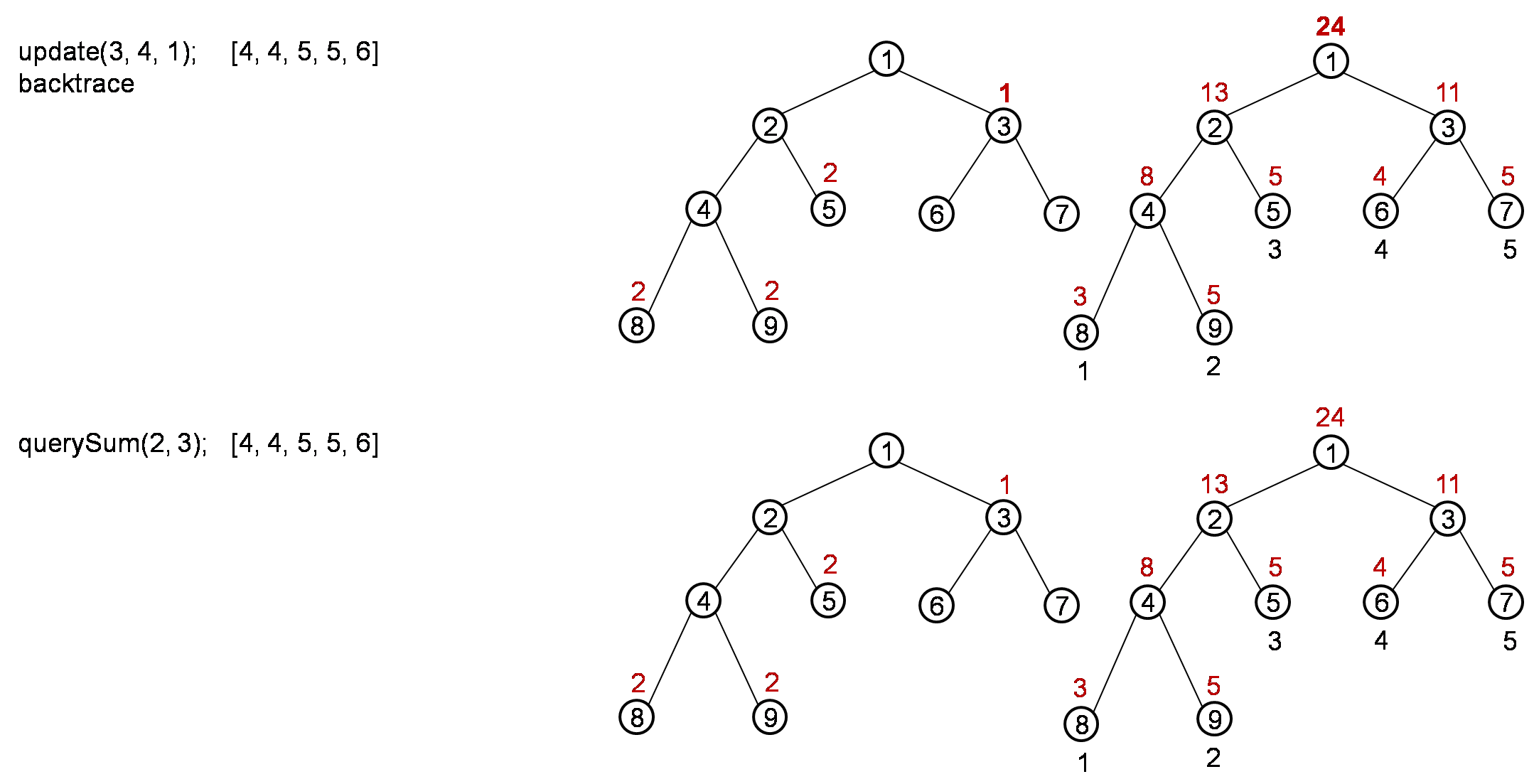
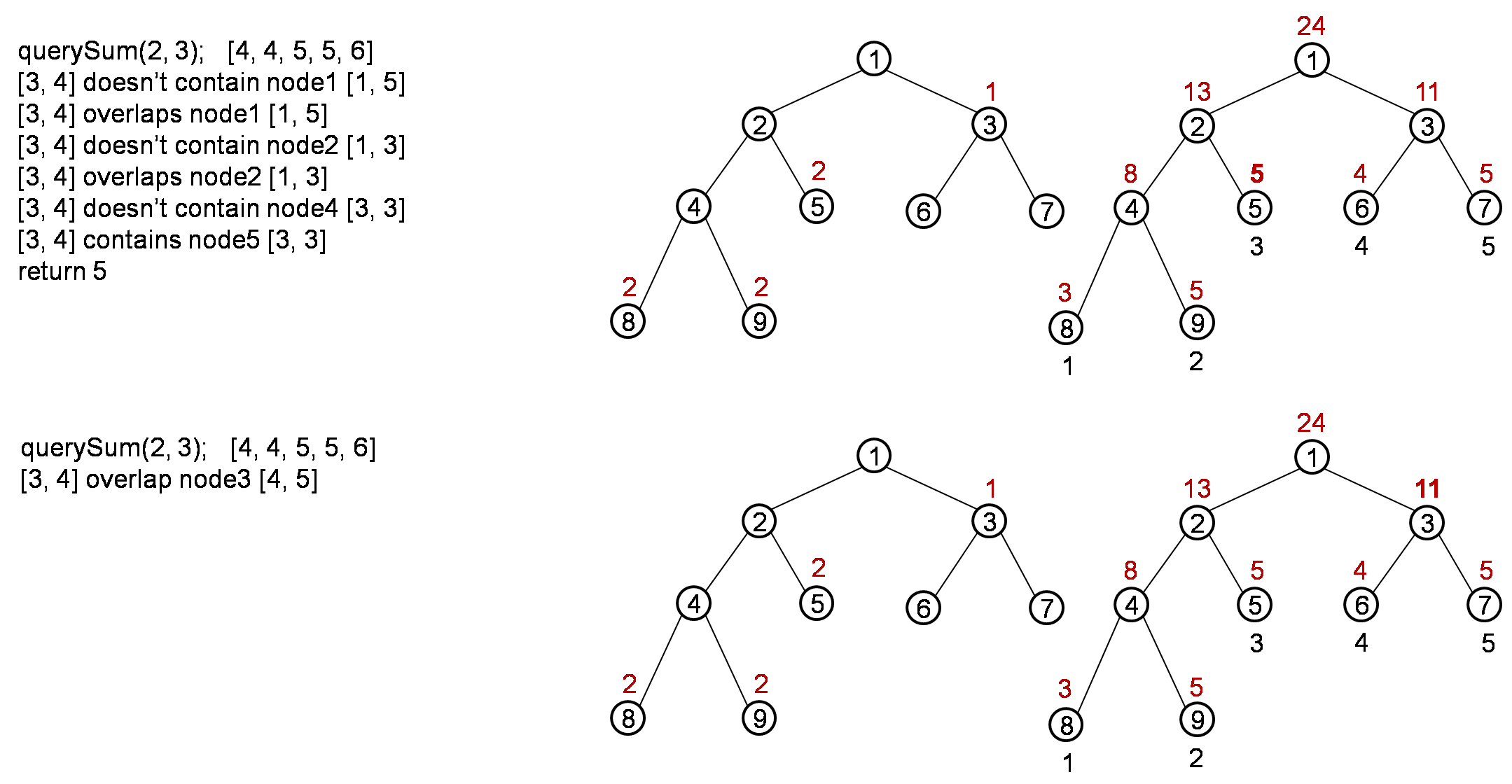
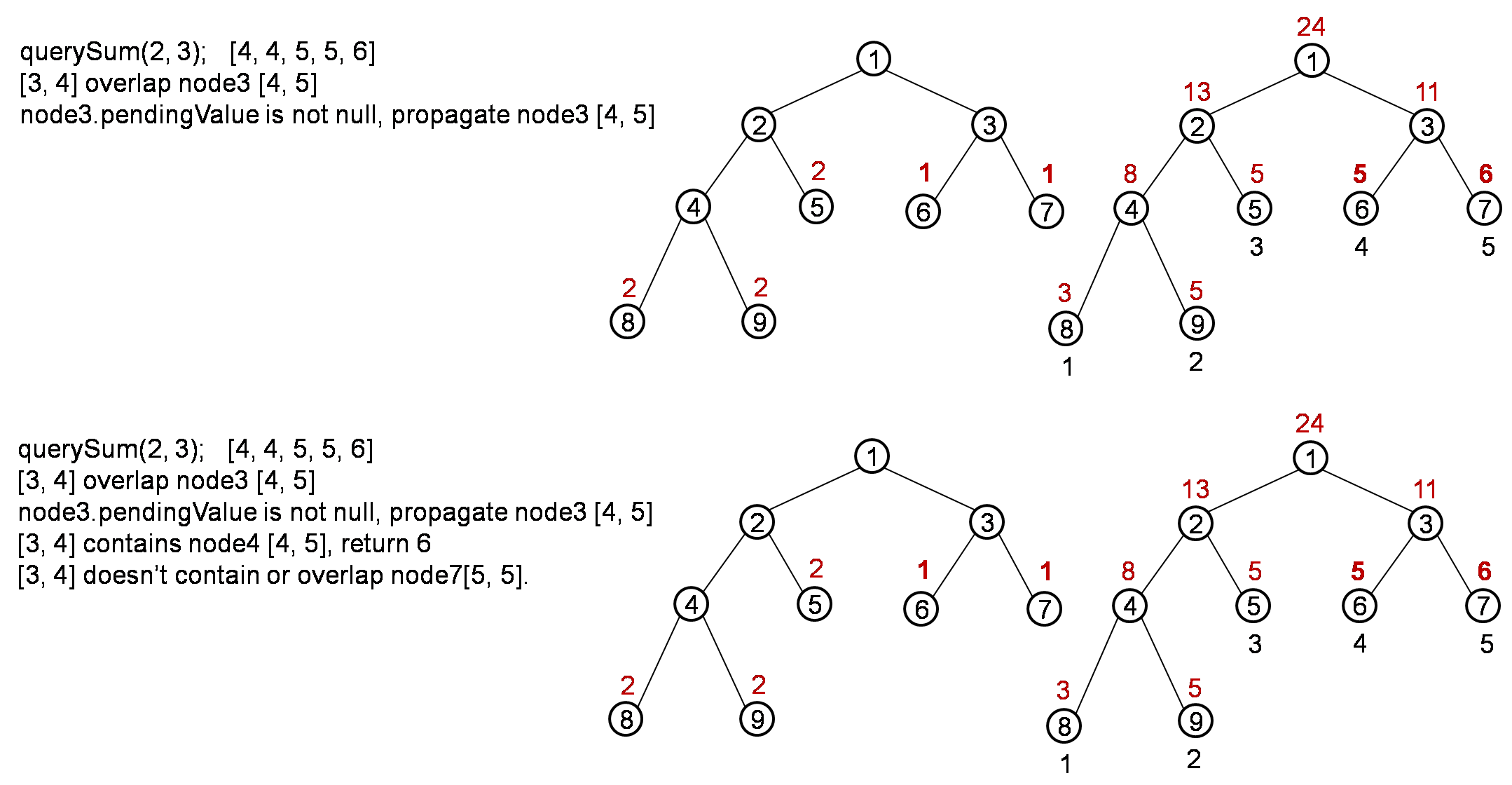
After the whole process, it should return result 10.

Segment tree has its advantage for range query in O(logN) time plus O(NlogN) storage. However, its disadvantage is that 1. We should preprocess to build segment tree in O(N) time. 2. Segment tree is a static tree, which means it is not allowed to add a new element or delete an element.

Check my code on github: link

Additive Number

https://leetcode.com/problems/additive-number/

Additive number is a string whose digits can form additive sequence.

A valid additive sequence should contain at least three numbers. Except for the first two numbers, each subsequent number in the sequence must be the sum of the preceding two.

For example:
"112358" is an additive number because the digits can form an additive sequence: 1, 1, 2, 3, 5, 8.

1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8

"199100199" is also an additive number, the additive sequence is: 1, 99, 100, 199.

1 + 99 = 100, 99 + 100 = 199

Note: Numbers in the additive sequence cannot have leading zeros, so sequence 1, 2, 03 or 1, 02, 3 is invalid.

Given a string containing only digits '0'-'9', write a function to determine if it’s an additive number.

Solution
This is a permutation a like problem. The key to solve it is to build the first number and second number. Then we check if string is an additive number started by the 2 number. Let len1 is the length of number1, len2 for number2, n for length of string. So, the length of the next number should be greater than or equal to max(len1, len2). So we have condition that n – len1 + len2 >= max(len1, len2)

Then we should write isValid(String str, int i, int j) function to check if str is a additive number with first number [0,…,i], second number is [i+1,…,j]. When writing this function, we should eliminate exception number like ‘012’, ’01’. On the other hand, we should pay attention that ‘0’ is a valid number.

check my code on github: link

pascal triangle

https://leetcode.com/problems/pascals-triangle-ii/

Given an index k, return the kth row of the Pascal’s triangle.

For example, given k = 3,
Return [1,3,3,1].

Analysis
Matrix like below is a pascal triangle p[][]. For row i, column j, p[i][j] it has value C(i, j) [Binomial Coefficient].

pascaltriangle

Below is the formula which can help us get C(n, m) from C(n, m – 1).

pascaltriangle2

In this way, we can get elements in row i in O(n) time.

check my code on github: link

Best Time to Buy and Sell Stock with Cooldown

https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:

prices = [1, 2, 3, 0, 2]
maxProfit = 3
transactions = [buy, sell, cooldown, buy, sell]

Solution 1
t is quite similar to balloon burst problem. We build a 2-dimension dp[][]. dp[left][right] indicates the max profit we can get from prices[left] to prices[right]. Because there is one day cool down, we can get the basic formula dp[left][right] = dp[left][k-1] + dp[k+1][right]. It means when we sold at k-1 time, at most we can but at k+1 time.
sellstockcooldown1
Complete formula is sellstockcooldown2
This solution takes O(n^2) time and space, which was not able to pass leetcode.

Solution 2
We define sell[] and notsell[]. sell[i] is the max profit if we sell at i time. notsell[i] is the max profit if we don’t sell at i time.

For sell[i], If we sell at i time, at least we should add the gap value of prices[i] – price[i – 1]. It has 2 conditions. When i-1 time was sold, then buy at i-1 time again and sell it at i time.(or it equal we didn’t sell at i-1 time, we passed it). So we have sell[i] = sell[i – 1] + prices[i] – price[i – 1].
Another condition is that at i-1 time, we didn’t sell. We really bought at i-1 time and sell at i time. Because there is a cool down time. i-2 time shouldn’t sell neither. So for this condition we have notsell[i – 2] + prices[i] – price[i – 1].
For notsell[i], it is a easy one. notesell[i] = max(sell[i – 1], notsell[i – 1])

Totally, we have:
sell[i] = max(sell[i – 1] + prices[i] – price[i – 1], notsell[i – 1] + prices[i] – price[i – 1])
notesell[i] = max(sell[i – 1], notsell[i – 1])

In the end, we return max(sell[n – 1], notsell[n – 1]). Below is a calculation matrix for [1, 2, 3, 0, 2].sellstockcooldown3

check my code on github: link

Minimum height trees

https://leetcode.com/problems/minimum-height-trees/

For a undirected graph with tree characteristics, we can choose any node as the root. The result graph is then a rooted tree. Among all possible rooted trees, those with minimum height are called minimum height trees (MHTs). Given such a graph, write a function to find all the MHTs and return a list of their root labels.

Format
The graph contains n nodes which are labeled from 0 to n – 1. You will be given the number n and a list of undirected edges (each edge is a pair of labels).

You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

Example 1:

Given n = 4, edges = [[1, 0], [1, 2], [1, 3]]

0
|
1
/ \
2 3
return [1]

Example 2:

Given n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]

0 1 2
\ | /
3
|
4
|
5
return [3, 4]

Solution 1: Since this is a tree like graph. It means there is circle. One solution is to delete leaf nodes in the graph. In the new graph, delete the leaf node again. Do this until graph only has 1 or 2 nodes. The left 1, 2 node are the result. check my code on github: link

Solution 2: Find a random node. Treat this node as root. And find the diameter path. The middle 2 nodes will be the result. check my previous code for finding diameter in binary tree: link

Both of the solution has time complexity O(V), space complexity O(V).