Monthly Archives: December 2015

Three tuple structure for sparse matrix, transpose and multiplication

When there are less than 1% non-zero elements in matrix, we call this matrix sparse matrix. Because there are so many 0s in matrix. An efficient way to store sparse matrix is to use three tuple data structure. It stores each non-zero element in matrix. A tuple shows a matrix[i][j]’s value in matrix.

public class Tuple {
    int i;
    int j;
    int value;
}

In this way, data structure for sparse matrix is like:

public class TSMatrix {
    public int rowNum;  // row length
    public int colNum;  // column length
    public Tuple[] datas;
}

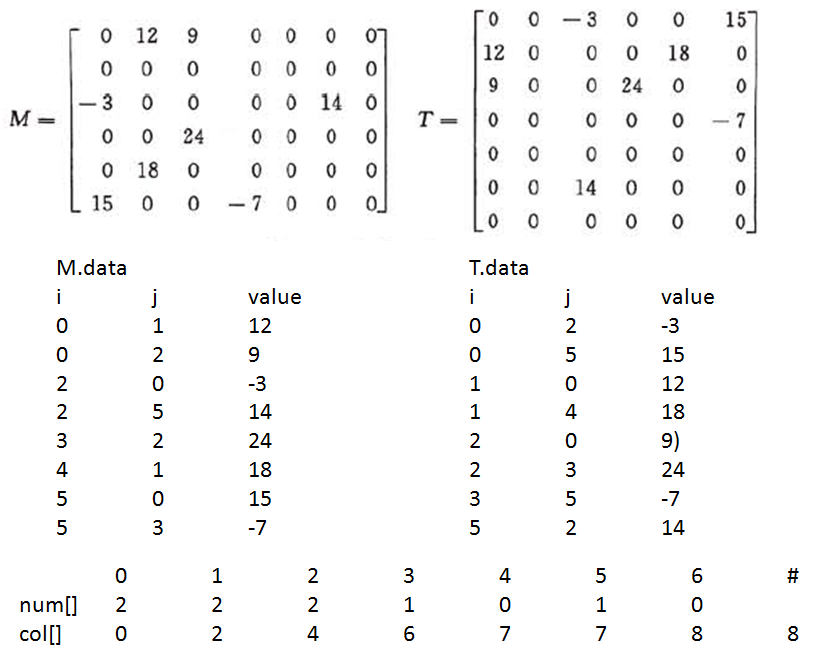
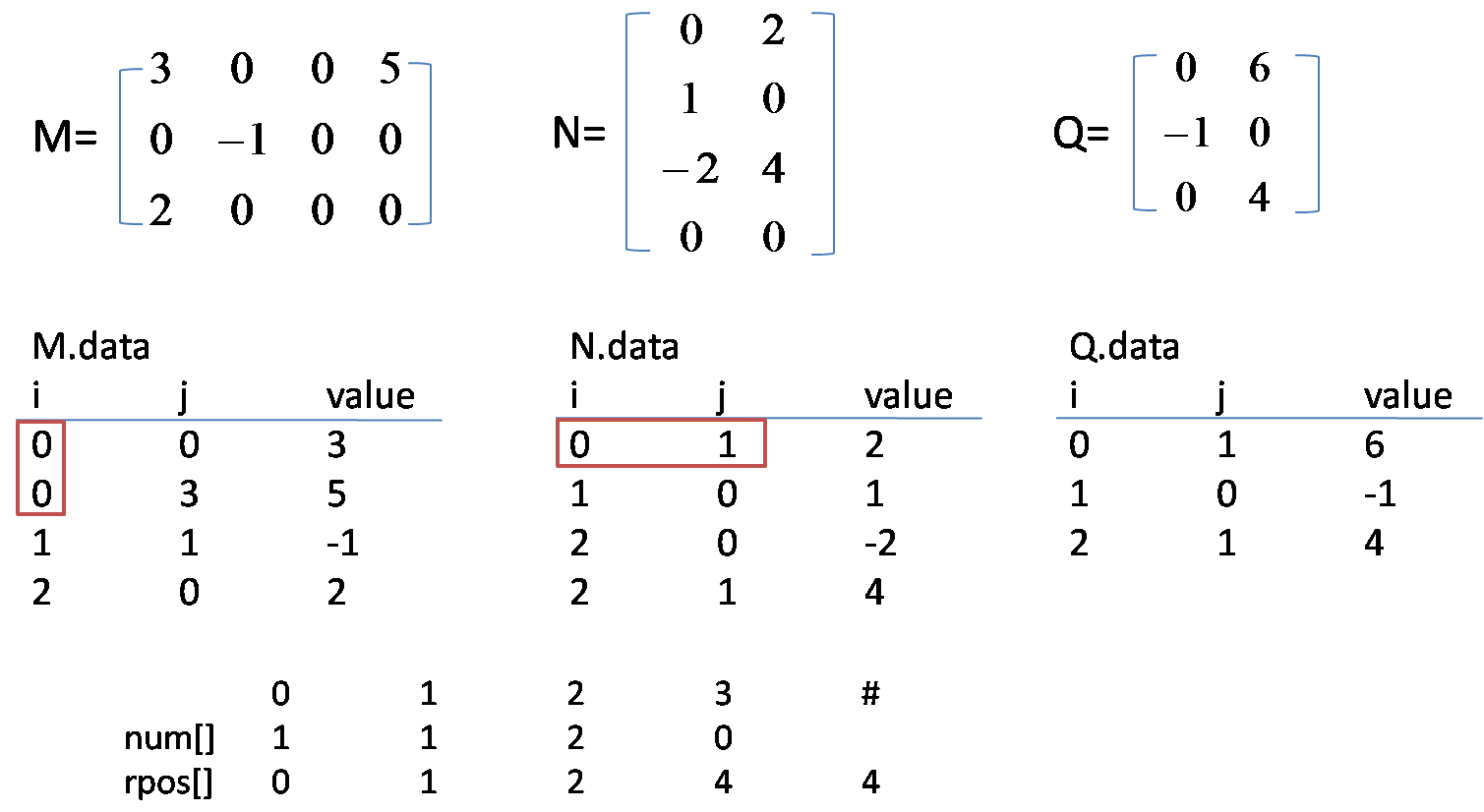
Two classical algorithm for sparse matrix are transpose and multiplication. For transpose, the key is that we should build col. Col[i] tells in new transposed matrix, row[i] start at datas[col[i]]. For multiplication,  the key is to build rpos[], rpos[i] means in matrix N row i starts at rpos[i] position in datas[].
Below picture shows process for transpose:

transpose

Below shows the process for 2 triple tuple matrix multiplication:

sparsematrixmultiplication

check my code on github: link

Deep Iterator

Write an Iterator that takes a nested(deep) list and flattens it out. For e.g. Collection A = {1, 2, {3, 4, 5, {6, 7}, {8,9}}, 10} When you call
DeepIterator it = new DeepIterator(A) ;
while(it.hasNext()){
System.out.println(it.next);
}

The key part of this problem is that the processed data is Collection type, which is the rawest type. It can contain anything.
We can treat it as a tree. The problem will change to traverse the leaf node in tree. So traversal a tree’s leaf node is straight forward. We can use stack to do preorder traversal.

However, we notice that a Collection has Collection.iterator(). This helps a lot. We put Iterator in stack. For each node’s children, we only store an iterator. In this way, space complexity is the deep of the tree.

check my code on github: link

Number of combination of triangle

Given an array with all positive numbers.
Find how many number of group are there which is able to make a triangle.
For example,
Given {3, 4, 5}, return 1
Given {3, 4, 5, 6}, return 4. Possible triangles are: {4, 5, 6}, {3, 5, 6}, {3, 4, 6}, {3, 4, 5}

The solution is that make 3 pointers, i<j<k. For each group of i, j, find the k position, where k is the first position at the right of j,  wherearr[i]+arr[j]<=arr[k]. In this way arr[i], arr[j], arr[[j+1, j+2,…,k-1]] can group a triangle.

Take arr={4, 5, 6, 7, 8, 9, 10} for example, the 3 pointers moving is like below:

The tricky part is that for each round of i, the k keeps moving to right, never moves back to left. We can use this to do k++ in each round of j.

check my code on github: link

Find min distance of two list

Given two sorted list, find the min distance of any 2 elements in 2 lists.
For example,
{1, 10, 20} and {5, 15, 21} min=21-20=1
{1, 10} and {15, 21} min=15-10=5

Solution 1 is to use merge sort. Compare abs(arr1[i]-arr[2] ) and min.

Solution 2 is that it doesn’t compare in each merge. It only compares when merge list changes. Here I say merge list is where min element from in each step.

Take arr1=[1, 2, 3, 4, 8], arr2=[7, 8, 9, 10] as example, the process is like below:

check my 2 solutions on github: link

regular expression (dp solution) 

'.' Matches any single character.
'*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

The function prototype should be:
bool isMatch(const char *s, const char *p)

Some examples:
isMatch("aa","a") → false
isMatch("aa","aa") → true
isMatch("aaa","aa") → false
isMatch("aa", "a*") → true
isMatch("aa", ".*") → true
isMatch("ab", ".*") → true
isMatch("aab", "c*a*b") → true

I wrote in recursion way to solve this problem before. This time I use dp. Let str=”0″+str, reg=”0″+reg. Build dp[][] boolean array with str.length+1 and reg.length+1 for row and column separately. dp[i][j]=true means str[1…i] match reg[1…j]. dp rules are as below: If reg.charAt[j] is not ‘.’ or ‘*’, dp[i][j]=dp[i-1][j-1] && reg.charAt(i)==str.chartAt(j) If reg.charAt[j]==‘.’, dp[i][j]=dp[i-1][j-1] If reg.charAt[j]==‘*’, (1)if dp[i-2][j] is true, then dp[i][j]=true. This considers * has 0 times. (2)If dp[i-1][j+1]==true, move from dp[i][j+1]to right until str[j]!=reg[i-1]. This considers * has 1, 2, or more times. 

public static boolean isMatch(String s, String p) {
    s = "$" + s;
    p = "$" + p;
    boolean[][] dp = new boolean[p.length()][s.length()];
    dp[0][0] = true;
    for (int i = 1; i < p.length(); i++) {
        if (p.charAt(i) == '.') {
            for (int j = 1; j < s.length(); j++) {
                dp[i][j] = dp[i - 1][j - 1];
            }
        }
        else if (p.charAt(i) != '*') {
            for (int j = 1; j < s.length(); j++) {
                dp[i][j] = dp[i - 1][j - 1] && p.charAt(i) == s.charAt(j);
            }
        }
        else {  // handle with '*'
            for (int j = 0; j < s.length(); j++) {
                boolean fromTop = dp[i - 1][j] || (i > 1 && dp[i - 2][j]);
                boolean fromLeft = j > 0 && dp[i][j - 1] && (p.charAt(i - 1) == '.' || p.charAt(i - 1) == s.charAt(j));
                dp[i][j] = fromTop || fromLeft;
            }
        }
    }
    return dp[p.length() - 1][s.length() - 1];
}

check my code on github: link

opg for The four operations

This is a pratice for computing basic +-*/ and () operations by opg algorithm.

Input 2*(3+4) should return 14
Input 2-+ should return Integer.MIN_VALUE

It is relatively easy to get the operator matrix like below. For eash, I ignore of using regular grammar, first, follow set to get this matrix.

       0   1   2   3   4   5   6
       +   -   *   /   (   )   #
0  +   <   <   <   <   >   <   na
1  -   <   <   <   <   >   <   na
2  *   >   >   <   <   >   <   na
3  /   >   >   <   <   >   <   na
4  (   >   >   >   >   >   na  na
5  )   <   <   <   <   =   <   na
6  #   <   <   <   <   na  <   na

The matrix[i][j] means when operator j is going to enter stack, and the stack top operator is operator i, the relationship between i and j. One thing to notice is that operators relationship is not symmetric. For example, we have ‘+’ < ‘-‘ and ‘-‘ < ‘+’.

Then, we maintain 2 stacks: number stack and operator stack. Every time, we compare next operator and top operator in stack. If next operator is less than top operator, then we pop number and operator stack to calculate. The result send back to number stack. If next operator is greater than top operator, then push next operator to operator stack. If equal, then pop operator stack. If nothing applied, it means there is a mistake.

This operator matrix doesn’t has number i as an operator. So we should avoid invalid string like “3(2+1)” or “(1+2)3”.

check my code on github: link

Simple regular expression

This is from leetcode:

'.' Matches any single character.
'*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

The function prototype should be:
bool isMatch(const char *s, const char *p)

Some examples:
isMatch("aa","a") → false
isMatch("aa","aa") → true
isMatch("aaa","aa") → false
isMatch("aa", "a*") → true
isMatch("aa", ".*") → true
isMatch("ab", ".*") → true
isMatch("aab", "c*a*b") → true

I used recursion to solve this problem. check my code on github: link

Suffix tree and ukkonen’s algorithm

It’s a long time that I spend to comprehend building suffix tree by ukkonen’s algorithm. Here I summarize some major point of this algorithm.

1. Suffix link. A internal node(t1, t2, t3,…,tn) has a suffix link. It points to another internal node or root which it’s a node for t2, t3, …, tn
2. Phase. When building a suffix tree, variable i loop from 0 to str.length()-1. For each different i, it is called a phase.
3. Length=0. At phase i, active length is 0, check if there is a pat charAt(i) at root.
4. Internal node not at root suffix link. At phase i, when a internal node is created and active point is not root. At the beginning when a internal A created, internal node points to root. When there is another internal node B created after A in the same phase, A points to the B by suffix link. And it goes on and on.
5. Internal node at root. At phase i, when a internal node is created, acitve point is root and active length is greater than 0. activeLength–, activeEdge++.
6. Update active point at root. Every time when we updated active point and when active point is root, we should update active point. There is chance that new active point change to other internal node after update.

In below example, after internal node M is created, do activeEdge++, activeLength–. We got (activePoint=root, activeEdge=2, activeLength=3). Since it is root, we should update active point. We move 3 chars from position 2(which is s). We move through ssi from root, then we arrived (activePoint=L, activeEdge=3, activeLength=2)

Below is my summary how we split to a internal node in 3 different scenario.

A full structure for mississipi without suffix link:

Here is my code for the suffix tree for below functions: link
1. substring position
2. longest common substring by generalized suffix tree
3. longest palindrome substring
4. longest repeated substring

This is a great video for suffix tree from Tushar: link

Another website to print suffix tree, link We can use this to verify the correctness of our code.

Tallest box

Given n boxes with length and width. A box with smaller length and smaller width can be put on a box with larger length and larger width.
Each box height is 1. Find the tallest box that they can put together. In general, we can build the box with m-dimension.
For example, if we have:
boxes = {
{0, 0},
{1, 2},
{1, 1},
{3, 4},
{4, 3},
{4, 4},
{3, 3} };
A longest possible combination is: (4, 4)->(3, 4)->(3, 3)->(1, 2)->(1, 1)->(0, 0). So tallest height is 6.

For n boxes, we do comparison between each box. If box[j] can be put on box[i], then we put an edge from box[i]->box[j].
In this way, we build a graph among boxes. Gathering all the boxes which doesn’t has parent, we use BFS to iterate.
The max number of iteration will be the result.

Assume a graph is like below, we can see the total iteration starting from v1, v2 to the end is 4.

Check my code on github: link

Sum of Set

Given a integer array, and a number n. Return true if n can be consisted by a subset of array.
For example, arr[]={3, 2, 3, 5}, n=11, return true; arr[]={3, 2, 3, 5}, n=12, return false

This problem can be solved by HashSet. Loop element i in arr[]. For each loop, get the value of sum i and each element in hashset. And put the value in hashset again. And put element i in hashset at the end of loop.

Check my code on github: link