Candy

leetcode 135.

There are N children standing in a line. Each child is assigned a rating value.

You are giving candies to these children subjected to the following requirements:

• Each child must have at least one candy.
• Children with a higher rating get more candies than their neighbors.

What is the minimum candies you must give?

Solution. This problem can be easily solved by scanning the array from left to right, right to left in O(n) time and O(n) space.

But there is a O(n) time, O(1) space solution, which is pretty hard to understand. Let me try to explain this O(1) space solution.

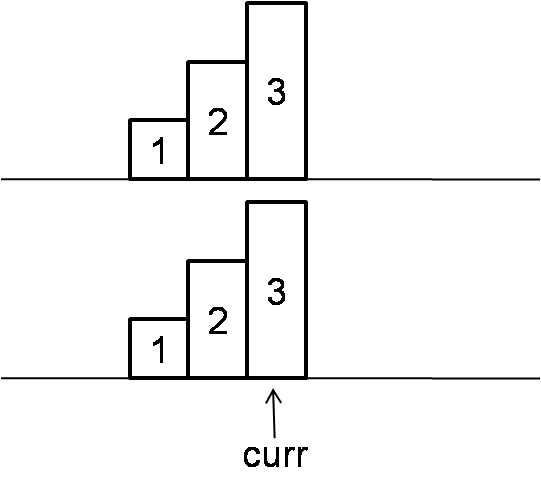
If current rating is greater than previous one, then current value should be prev + 1

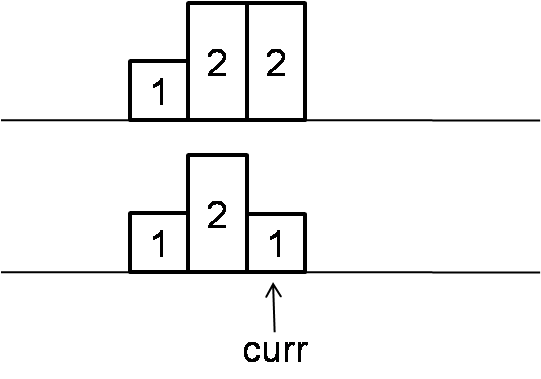
If current rating is equal to previous one, then current value should be 1

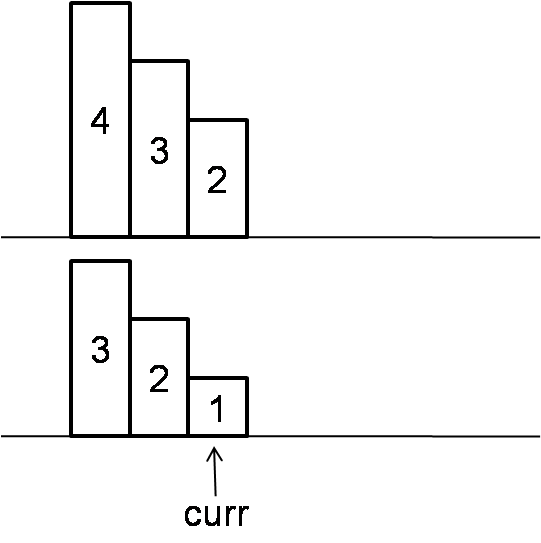
If current rating is less than previous one, we don’t know the value yet.

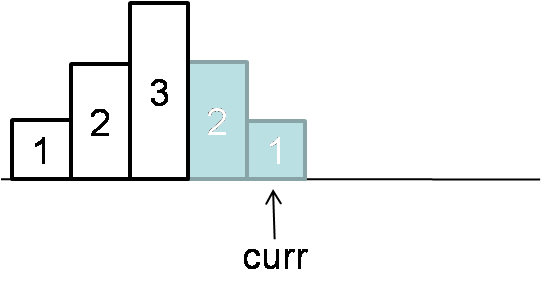
Let’s consider the continuous descending ratings. If there is continuous descending ratings, we will use countDown to memorize the descending length. Below case, countDown = 2 at curr position.

During a descending order, when curr is equal to previous or greater than previous, we can use progression formula to calculate the descending area size.

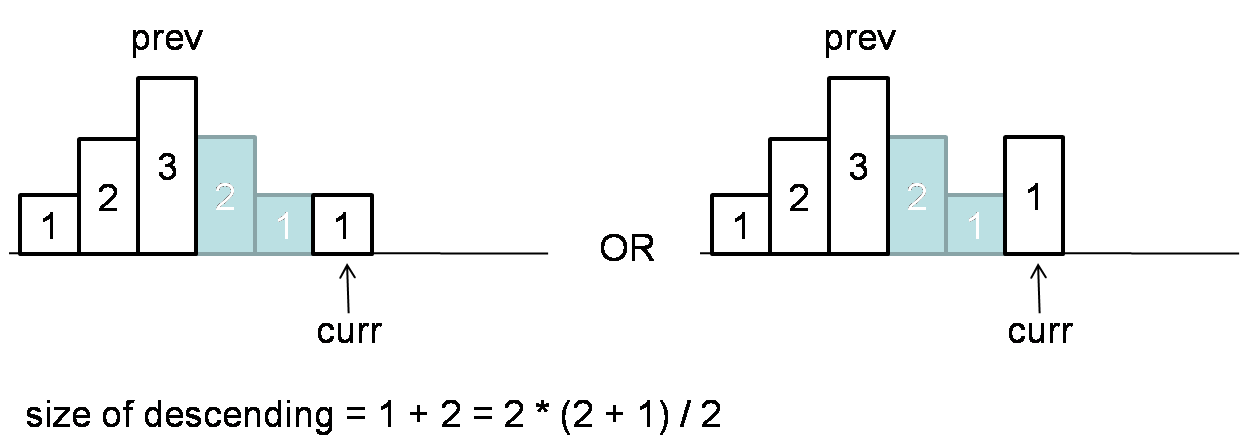
Let’s reconsider the prev when calculating size of descending area. Think about below case. Prev is 2, which is not tall enough and makes next 2 elements to 1 and 0.

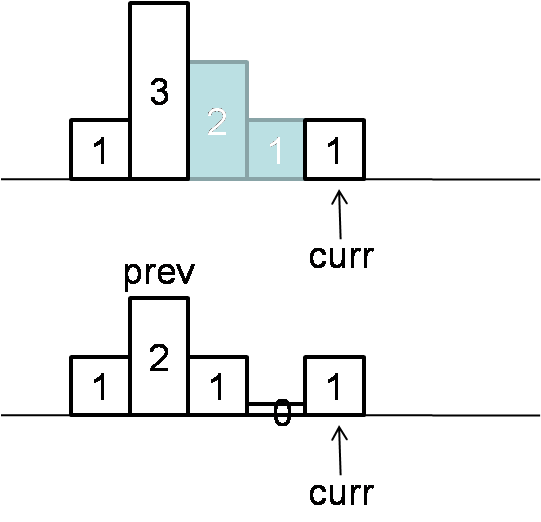
In this case when countDown >= prev, we should increase prev by countDown – prev + 1.

The final code is like below:

public static int candy(int[] ratings) {
    int pre = 1, countDown = 0, total = 1;
    for (int i = 1; i < ratings.length; i++) {
        if (ratings[i] >= ratings[i - 1]) {
            if (countDown > 0) {
                total += countDown * (countDown + 1) / 2;   // progression part
                if (countDown >= pre) { // check if pre is tall enough
                    total += countDown - pre + 1;
                }
                pre = 1;    // when ascending and there is countDown, prev should be 1
                countDown = 0;
            }
            pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;   // when equals to previous one, set to 1. Else set to prev + 1
            total += pre;
        }
        else {
            countDown++;
        }
    }
    if (countDown > 0) {    // check if there is countDown in the end
        total += countDown * (countDown + 1) / 2;
        if (countDown >= pre) {
            total += countDown - pre + 1;
        }
    }
    return total;
}

Check my code on github.